Page 262 - Schaum's Outline of Theory and Problems of Signals and Systems

FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS 25 1

From Eq. (5.142) it follows that

e-j"~' H 2rTTS(o + wo)

From Euler's formula we have
+
COS mot = L (e~"'~' e-~w~')
2
Thus, using Eqs. (5.142) and (5.143) and the linearity property (5.49), we get

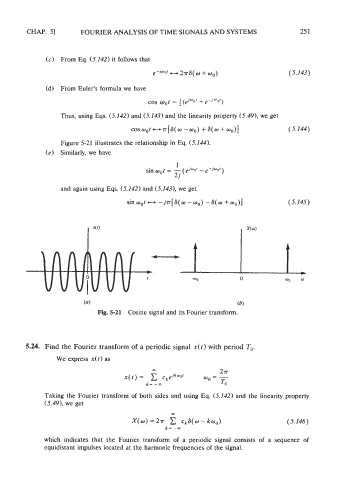
cos wot - ~[6(w - w,,) + 6(w + wo)] (5.144)
Figure 5-21 illustrates the relationship in Eq. (5.144).
Similarly, we have

and again using Eqs. (5.142) and (5.143), we get

sin wot - - j.rr[S(o - wo) - 6(w + wo)] (5.145)

(b)
Fig. 5-21 Cosine signal and its Fourier transform.

5.24. Find the Fourier transform of a periodic signal x(t) with period To.
We express x(t ) as

Taking the Fourier transform of both sides and using Eq. (5.142) and the linearity property
(5.49), we get

which indicates that the Fourier transform of a periodic signal consists of a sequence of
equidistant impulses located at the harmonic frequencies of the signal.