Page 330 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 61 FOURIER ANALYSIS OF DISCRETE-TIME SIGNALS AND SYSTEMS 317

By the change of variable m = n - no, we obtain

Hence,

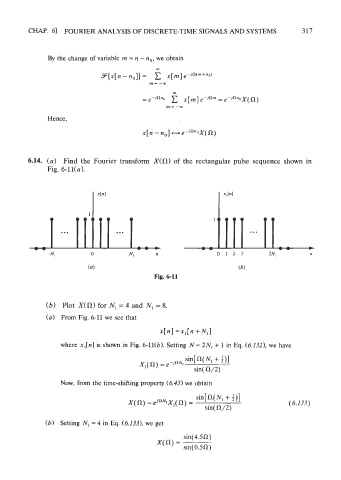
6.14. (a) Find the Fourier transform X(0) of the rectangular pulse sequence shown in
Fig. 6-1 l(a).

(b)
Fig. 6-1 1

(b) Plot X(R) for N, = 4 and N, = 8.
(a) From Fig. 6-11 we see that

x[n] =x,[n + N,]

where x,[n] is shown in Fig. 6-ll(b). Setting N = 2N1 + 1 in Eq. (6.132), we have

Now, from the time-shifting property (6.43) we obtain

(b) Setting N, = 4 in Eq. (6.133), we get