Page 184 - Schaum's Outlines - Probability, Random Variables And Random Processes

RANDOM PROCESSES

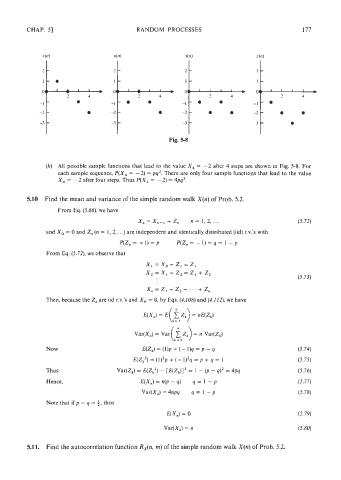
Fig. 5-8

(b) All possible sample functions that lead to the value X, = -2 after 4 steps are shown in Fig. 5-8. For
each sample sequence, P(X, = -2) = pq3. There are only four sample functions that lead to the value
X, = -- 2 after four steps. Thus P(X, = - 2) = 4pq3.

5.10 Find the mean and variance of the simple random walk X(n) of Prob. 5.2.
From Eq. (5.66), we have

and X, = 0 and 2, (n = 1,2, . . .) are independent and identically distributed (iid) r.v.'s with

From Eq. (5.72), we observe that

Then, because the 2, are iid r.v.3 and Xo = 0, by Eqs. (4.108) and (4.1 12), we have

)
Var(X,) = Var 1 Z, = n Var(Z,)
Now

Thus
Hence.

Note that if p = q = i, then

5.11. Find the autocorrelation function R,(n, rn) of the simple random walk X(n) of Prob. 5.2.