Page 121 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

The Electronic System
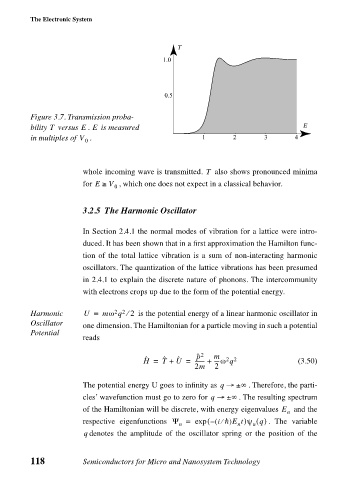
1.0 T

0.5

Figure 3.7. Transmission proba-
E
E
T
bility versus . is measured E
in multiples of V . 1 2 3 4
0
T
whole incoming wave is transmitted. also shows pronounced minima
for E ≥ V , which one does not expect in a classical behavior.
0

3.2.5 The Harmonic Oscillator

In Section 2.4.1 the normal modes of vibration for a lattice were intro-
duced. It has been shown that in a first approximation the Hamilton func-
tion of the total lattice vibration is a sum of non-interacting harmonic
oscillators. The quantization of the lattice vibrations has been presumed
in 2.4.1 to explain the discrete nature of phonons. The intercommunity
with electrons crops up due to the form of the potential energy.

Harmonic U = mω q ⁄ 2 is the potential energy of a linear harmonic oscillator in
2 2
Oscillator one dimension. The Hamiltonian for a particle moving in such a potential
Potential
reads

2
p ˆ
ˆ
ˆ
ˆ
----ω q
H = T + U = ------- + m 2 2 (3.50)
2m 2
The potential energy U goes to infinity as q → ± ∞ . Therefore, the parti-
cles’ wavefunction must go to zero for q → ± ∞ . The resulting spectrum
of the Hamiltonian will be discrete, with energy eigenvalues E and the
n
⁄
respective eigenfunctions Ψ = exp ( – ( i —)E t)ψ q() . The variable
n n n
q denotes the amplitude of the oscillator spring or the position of the
118 Semiconductors for Micro and Nanosystem Technology