Page 176 - Sensing, Intelligence, Motion : How Robots and Humans Move in an Unstructured World

MAXIMUM TURN STRATEGY 151

x
1 2 v t b
v 0 v 0 max
V
II

I

−r u
v′ 0 v′′ 0 v max V 0
(a) (b)
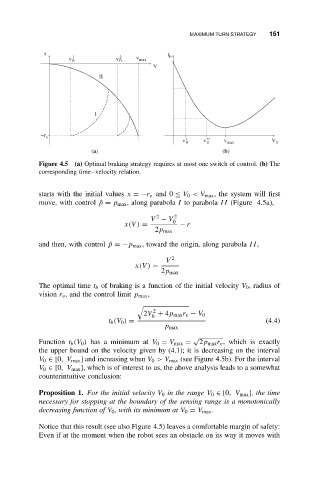
Figure 4.5 (a) Optimal braking strategy requires at most one switch of control. (b) The
corresponding time–velocity relation.

starts with the initial values x =−r v and 0 ≤ V 0 <V max , the system will first
move, with control ˆp = p max , along parabola I to parabola II (Figure 4.5a),
2
V − V 0 2
x(V ) = − r
2p max
and then, with control ˆp =−p max , toward the origin, along parabola II,

V 2
x(V ) =
2p max
The optimal time t b of braking is a function of the initial velocity V 0 ,radiusof
vision r v , and the control limit p max ,

2
2V + 4p max r v − V 0
0
t b (V 0 ) = (4.4)
p max
√
Function t b (V 0 ) has a minimum at V 0 = V max = 2p max r v , which is exactly
the upper bound on the velocity given by (4.1); it is decreasing on the interval
V 0 ∈ [0,V max ] and increasing when V 0 >V max (see Figure 4.5b). For the interval
V 0 ∈ [0,V max ], which is of interest to us, the above analysis leads to a somewhat
counterintuitive conclusion:

Proposition 1. For the initial velocity V 0 in the range V 0 ∈ [0,V max ], the time
necessary for stopping at the boundary of the sensing range is a monotonically
decreasing function of V 0 , with its minimum at V 0 = V max .

Notice that this result (see also Figure 4.5) leaves a comfortable margin of safety:
Even if at the moment when the robot sees an obstacle on its way it moves with