Page 224 - Sensing, Intelligence, Motion : How Robots and Humans Move in an Unstructured World

PLANAR REVOLUTE–REVOLUTE (RR) ARM 199

(a)

T
S

(b) (c)

(d) (e)
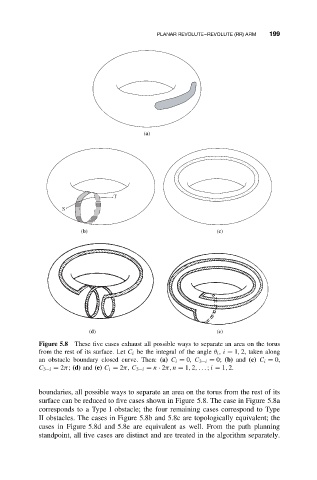
Figure 5.8 These five cases exhaust all possible ways to separate an area on the torus
from the rest of its surface. Let C i be the integral of the angle θ i , i = 1, 2, taken along
an obstacle boundary closed curve. Then: (a) C i = 0, C 3−i = 0; (b) and (c) C i = 0,
C 3−i = 2π; (d) and (e) C i = 2π, C 3−i = n · 2π, n = 1, 2,... ; i = 1, 2.

boundaries, all possible ways to separate an area on the torus from the rest of its
surface can be reduced to five cases shown in Figure 5.8. The case in Figure 5.8a
corresponds to a Type I obstacle; the four remaining cases correspond to Type
II obstacles. The cases in Figure 5.8b and 5.8c are topologically equivalent; the
cases in Figure 5.8d and 5.8e are equivalent as well. From the path planning
standpoint, all five cases are distinct and are treated in the algorithm separately.