Page 543 - Sensors and Control Systems in Manufacturing

496
Cha p te r

5.26 5 T e n 4.54 4.35 4.17 4 3.85 3.7 3.57 3.45 Wavelength (um)
4.76
0.01
1900 2000 2100 2200 2300 2400 2500 2600 2700 2800 2900 Wavenumber
(cm–1)
Source
Temperature (K)
0.001
373
573
W/(cm 2 sr cm –1 ) 773
0.0001
973
1173
0.00001
1373
1573
0.000001
0.0000001
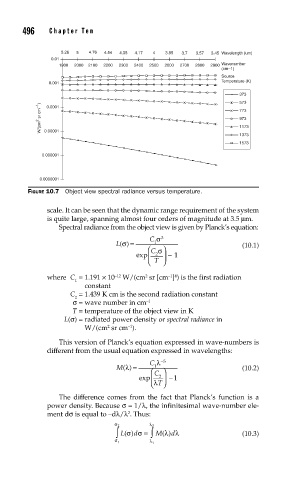
FIGURE 10.7 Object view spectral radiance versus temperature.

scale. It can be seen that the dynamic range requirement of the system
is quite large, spanning almost four orders of magnitude at 3.5 μm.
Spectral radiance from the object view is given by Planck’s equation:
C σ 3
1
L()σ = ⎛ C σ ⎞ (10.1)
exp ⎜ 2 ⎟ − 1
⎝ T ⎠

–12
–1 4
2
where C = 1.191 × 10 W/(cm sr [cm ] ) is the first radiation
1
constant
C = 1.439 K cm is the second radiation constant
2
σ = wave number in cm –1
T = temperature of the object view in K
L(σ) = radiated power density or spectral radiance in
2
W/(cm sr cm ).
–1
This version of Planck’s equation expressed in wave-numbers is
different from the usual equation expressed in wavelengths:
C λ −5
M()λ = ⎛ 1 C ⎞ (10.2)
exp⎜ 2 ⎟ −1
⎝ λ T ⎠
The difference comes from the fact that Planck’s function is a
power density. Because σ = 1/λ, the infinitesimal wave-number ele-
ment dσ is equal to –dλ/λ . Thus:
2
σ 2 λ 2
σ
=
λ
∫ L() dσ ∫ M( ) dλ (10.3)
σ 1 λ 1