Page 89 - Separation process principles 2

54 Chapter 2 Thermodynamics of Separation Operations

where energies of interaction Xij = Xji, but Xii f Xji Fol-
lowing the treatment by Orye and Prausnitz [36], substitu-
I 1 atrn
tion of the binary form of (2-75) into (2-65) and defining the
binary interaction parameters as

leads to the following equation for a binary system:

xethyl alcohol
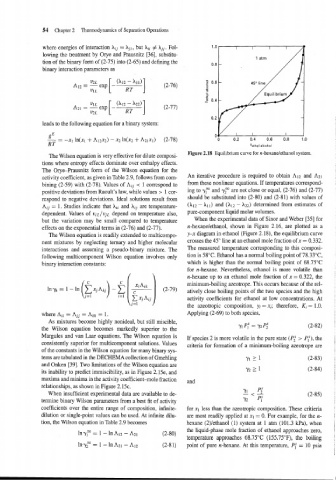
Figure 2.18 Equilibrium curve for n-hexanelethanol system.
The Wilson equation is very effective for dilute composi-
tions where entropy effects dominate over enthalpy effects.
The Orye-Prausnitz form of the Wilson equation for the
activity coefficient, as given in Table 2.9, follows from com- An iterative procedure is required to obtain A12 and A21
from these nonlinear equations. If temperatures correspond-
bining (2-59) with (2-78). Values of Aij < 1 correspond to
positive deviations from Raoult's law, while values > 1 cor- ing to ypO and ?? are not close or equal, (2-76) and (2-77)
respond to negative deviations. Ideal solutions result from should be substituted into (2-80) and (2-81) with values of
Aij = 1. Studies indicate that hii and Xij are temperature- (Al2 - All) and (h12 - X22) determined from estimates of
dependent. Values of viL/vjL depend on temperature also, pure-component liquid molar volumes.
but the variation may be small compared to temperature When the experimental data of Sinor and Weber [35] for
effects on the exponential terms in (2-76) and (2-77). n-hexanelethanol, shown in Figure 2.16, are plotted as a
The Wilson equation is readily extended to multicompo- y-x diagram in ethanol (Figure 2. IS), the equilibrium curve
nent mixtures by neglecting ternary and higher molecular crosses the 45" line at an ethanol mole fraction of x = 0.332.
interactions and assuming a pseudo-binary mixture. The The measured temperature corresponding to this composi-
following multicomponent Wilson equation involves only tion is 58°C. Ethanol has a normal boiling point of 78.33"C,
binary interaction constants: which is higher than the normal boiling point of 68.75"C
for n-hexane. Nevertheless, ethanol is more volatile than
n-hexane up to an ethanol mole fraction of x = 0.322, the
minimum-boiling azeotrope. This occurs because of the rel-
atively close boiling points of the two species and the high
activity coefficients for ethanol at low concentrations. At
the azeotropic composition, yi = xi; therefore, Ki = 1.0.
where Aii = Ajj = Akk = 1. Applying (2-69) to both species,
As mixtures become highly nonideal, but still miscible,
the Wilson equation becomes markedly superior to the
Margules and van Laar equations. The Wilson equation is
If species 2 is more volatile in the pure state (Pi > PS), the
consistently superior for multicomponent solutions. Values
criteria for formation of a minimum-boiling azeotrope are
of the constants in the Wilson equation for many binary sys-
tems are tabulated in the DECHEMA collection of Gmehling
and Onken [39]. Two limitations of the Wilson equation are
its inability to predict immiscibility, as in Figure 2.15e, and
maxima and minima in the activity coefficient-mole fraction
and
relationships, as shown in Figure 2.15~.
When insufficient experimental data are available to de-
termine binary Wilson parameters from a best fit of activity
coefficients over the entire range of composition, infinite- for xl less than the azeotropic composition. These critieria
dilution or single-point values can be used. At infinite dilu- are most readily applied at xl = 0. For example, for the n-
tion, the Wilson equation in Table 2.9 becomes hexane (2)lethanol (1) system at 1 atm (101.3 kPa), when
the liquid-phase mole fraction of ethanol approaches zero,
temperature approaches 68.75"C (155.75"F), the boiling
point of pure n-hexane. At this temperature, Pf = 10 psia