Page 351 - Shigley's Mechanical Engineering Design

bud29281_ch06_265-357.qxd 12/02/2009 7:26 pm Page 326 pinnacle s-171:Desktop Folder:Temp Work:Don't Delete (Jobs):MHDQ196/Budynas:

326 Mechanical Engineering Design
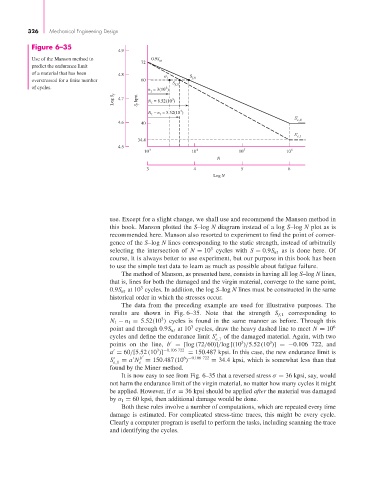
Figure 6–35
4.9
Use of the Manson method to 0.9S ut
72
predict the endurance limit
of a material that has been 4.8
overstressed for a finite number 60 1 S f,0
S f,1
of cycles. 3
n = 3(10 )
1
Log S f 4.7 S f kpsi N = 8.52(10 )
3
1
N – n = 5.52(10 ) 3
1 1
S' e,0
4.6 40
S' e,1
34.4
4.5
10 3 10 4 10 5 10 6
N
3 4 5 6
Log N

use. Except for a slight change, we shall use and recommend the Manson method in
this book. Manson plotted the S–log N diagram instead of a log S–log N plot as is
recommended here. Manson also resorted to experiment to find the point of conver-
gence of the S–log N lines corresponding to the static strength, instead of arbitrarily
3
selecting the intersection of N = 10 cycles with S = 0.9S ut as is done here. Of
course, it is always better to use experiment, but our purpose in this book has been
to use the simple test data to learn as much as possible about fatigue failure.
The method of Manson, as presented here, consists in having all log S–log N lines,
that is, lines for both the damaged and the virgin material, converge to the same point,
3
0.9S ut at 10 cycles. In addition, the log S–log N lines must be constructed in the same
historical order in which the stresses occur.
The data from the preceding example are used for illustrative purposes. The
results are shown in Fig. 6–35. Note that the strength S f,1 corresponding to
3
N 1 − n 1 = 5.52(10 ) cycles is found in the same manner as before. Through this
3
point and through 0.9S ut at 10 cycles, draw the heavy dashed line to meet N = 10 6
cycles and define the endurance limit S of the damaged material. Again, with two
e,1
3
3

points on the line, b = [log (72/60)]/log [(10 )/5.52 (10 )] =−0.106 722, and
3 −0.106 722

a = 60/[5.52 (10 )] = 150.487 kpsi. In this case, the new endurance limit is

6 −0.106 722
b

S = a N = 150.487 (10 ) = 34.4 kpsi, which is somewhat less than that
e,1 e
found by the Miner method.
It is now easy to see from Fig. 6–35 that a reversed stress σ = 36 kpsi, say, would
not harm the endurance limit of the virgin material, no matter how many cycles it might
be applied. However, if σ = 36 kpsi should be applied after the material was damaged
by σ 1 = 60 kpsi, then additional damage would be done.
Both these rules involve a number of computations, which are repeated every time
damage is estimated. For complicated stress-time traces, this might be every cycle.
Clearly a computer program is useful to perform the tasks, including scanning the trace
and identifying the cycles.