Page 349 - Shigley's Mechanical Engineering Design

bud29281_ch06_265-357.qxd 12/02/2009 7:23 pm Page 324 pinnacle s-171:Desktop Folder:Temp Work:Don't Delete (Jobs):MHDQ196/Budynas:

324 Mechanical Engineering Design
Cycle 3: r = 10/−30 =−0.333, and since σ m < 0, S f = S e , indefinite life follows and
N ← ∞
Cycle Number S f , kpsi N, cycles

3
1 70.3 619(10 )
2 67.5 ∞
3 67.5 ∞

From Eq. (6–58) the damage per block is

n i
1 1 1 N
D = = N 3 + + = 3
N i 619(10 ) ∞ ∞ 619(10 )
3
Answer Setting D = 1 yields N = 619(10 ) cycles.

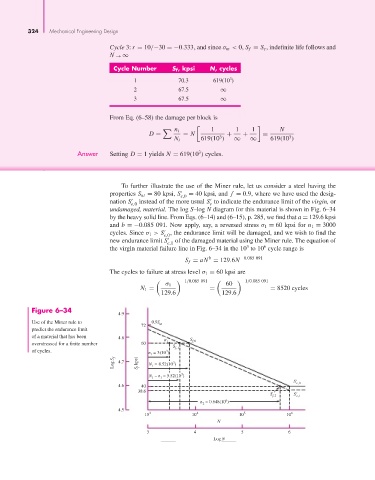
To further illustrate the use of the Miner rule, let us consider a steel having the
properties S ut = 80 kpsi, S = 40 kpsi, and f = 0.9, where we have used the desig-
e,0
nation S instead of the more usual S to indicate the endurance limit of the virgin, or

e,0 e
undamaged, material. The log S–log N diagram for this material is shown in Fig. 6–34
by the heavy solid line. From Eqs. (6–14) and (6–15), p. 285, we find that a = 129.6 kpsi
and b =−0.085 091. Now apply, say, a reversed stress σ 1 = 60 kpsi for n 1 = 3000
cycles. Since σ 1 > S , the endurance limit will be damaged, and we wish to find the

e,0
new endurance limit S of the damaged material using the Miner rule. The equation of
e,1
6
3
the virgin material failure line in Fig. 6–34 in the 10 to 10 cycle range is
b
S f = aN = 129.6N −0.085 091
The cycles to failure at stress level σ 1 = 60 kpsi are
−1/0.085 091 −1/0.085 091

σ 1 60
N 1 = = = 8520 cycles
129.6 129.6
Figure 6–34
4.9
Use of the Miner rule to 0.9S ut
72
predict the endurance limit
of a material that has been 4.8
1 S f,0
overstressed for a finite number 60 S
of cycles. n = 3(10 ) f,1
3
1
Log S f 4.7 S f kpsi N = 8.52(10 )
3
1
3
– n = 5.52(10 )
N 1
1
S' e,0
4.6 40
38.6
S S'
f,2 e,1
6
n = 0.648(10 )
2
4.5
10 3 10 4 10 5 10 6
N
3 4 5 6
Log N