Page 345 - Shigley's Mechanical Engineering Design

bud29281_ch06_265-357.qxd 11/30/2009 4:23 pm Page 320 pinnacle s-171:Desktop Folder:Temp Work:Don't Delete (Jobs):MHDQ196/Budynas:

320 Mechanical Engineering Design
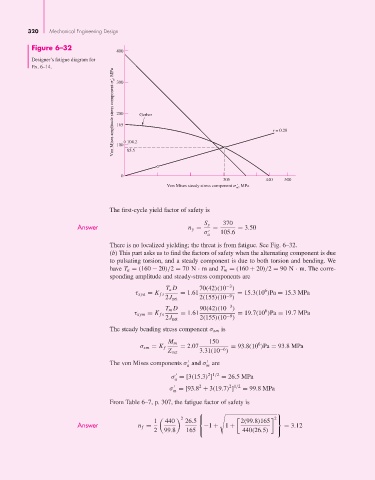
Figure 6–32
400
Designer’s fatigue diagram for
Ex. 6–14. ' 300
Von Mises amplitude stress component a , MPa 200 104.2 Gerber r = 0.28

165

100

0 85.5
305 440 500
'
Von Mises steady stress component , MPa
m

The first-cycle yield factor of safety is

Answer n y = S y = 370 = 3.50
σ 105.6
a
There is no localized yielding; the threat is from fatigue. See Fig. 6–32.
(b) This part asks us to find the factors of safety when the alternating component is due
to pulsating torsion, and a steady component is due to both torsion and bending. We
have T a = (160 − 20)/2 = 70 N · m and T m = (160 + 20)/2 = 90 N · m. The corre-
sponding amplitude and steady-stress components are
−3
T a D 70(42)(10 ) 6
τ xya = K fs = 1.61 −9 = 15.3(10 )Pa = 15.3MPa
2J net 2(155)(10 )
−3
T m D 90(42)(10 ) 6
τ xym = K fs = 1.61 −9 = 19.7(10 )Pa = 19.7MPa
2J net 2(155)(10 )
The steady bending stress component σ xm is
M m 150 6
σ xm = K f = 2.07 −6 = 93.8(10 )Pa = 93.8MPa
Z net 3.31(10 )
The von Mises components σ and σ are

a m
2 1/2
σ = [3(15.3) ] = 26.5MPa

a
2
2 1/2
σ = [93.8 + 3(19.7) ] = 99.8MPa

m
From Table 6–7, p. 307, the fatigue factor of safety is
⎧ ⎫

2

1 440 26.5 ⎨ 2(99.8)165 2⎬

Answer n f = −1 + 1 + = 3.12
2 99.8 165 ⎩ 440(26.5) ⎭