Page 367 - Shigley's Mechanical Engineering Design

bud29281_ch06_265-357.qxd 11/30/2009 4:24 pm Page 342 pinnacle s-171:Desktop Folder:Temp Work:Don't Delete (Jobs):MHDQ196/Budynas:

342 Mechanical Engineering Design
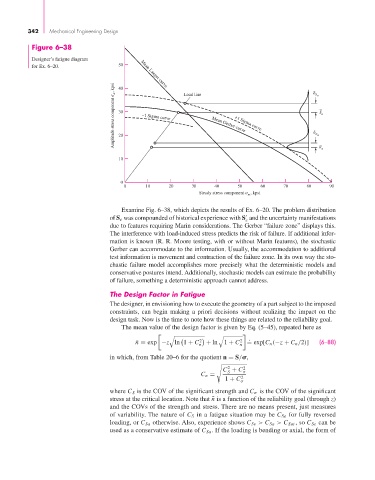
Figure 6–38

Designer’s fatigue diagram
for Ex. 6–20. 50 Mean Langer curve

Amplitude stress component a , kpsi 30 –1 Sigma curve Load line Mean Gerber curve S a _ S a
40

+1 Sigma curve
a
20
_
10 a

0
0 10 20 30 40 50 60 70 80 90
Steady stress component m , kpsi

Examine Fig. 6–38, which depicts the results of Ex. 6–20. The problem distribution

of S e was compounded of historical experience with S and the uncertainty manifestations
e
due to features requiring Marin considerations. The Gerber “failure zone” displays this.
The interference with load-induced stress predicts the risk of failure. If additional infor-
mation is known (R. R. Moore testing, with or without Marin features), the stochastic
Gerber can accommodate to the information. Usually, the accommodation to additional
test information is movement and contraction of the failure zone. In its own way the sto-
chastic failure model accomplishes more precisely what the deterministic models and
conservative postures intend. Additionally, stochastic models can estimate the probability
of failure, something a deterministic approach cannot address.

The Design Factor in Fatigue
The designer, in envisioning how to execute the geometry of a part subject to the imposed
constraints, can begin making a priori decisions without realizing the impact on the
design task. Now is the time to note how these things are related to the reliability goal.
The mean value of the design factor is given by Eq. (5–45), repeated here as

.
' '
2 2
¯ n = exp −z ln 1 + C + ln 1 + C = exp[C n (−z + C n /2)] (6–88)
n n
in which, from Table 20–6 for the quotient n = S/ ,
2
C + C 2 σ
S
C n =
1 + C 2
σ
where C S is the COV of the significant strength and C σ is the COV of the significant
stress at the critical location. Note that ¯n is a function of the reliability goal (through z)
and the COVs of the strength and stress. There are no means present, just measures
of variability. The nature of C S in a fatigue situation may be C Se for fully reversed
loading, or C Sa otherwise. Also, experience shows C Se > C Sa > C Sut , so C Se can be
used as a conservative estimate of C Sa . If the loading is bending or axial, the form of