Page 167 - Statistics for Dummies

Similarly for Problem 2, p(X > 24) becomes
And Problem 3 translates from p(16 < X < 24) to
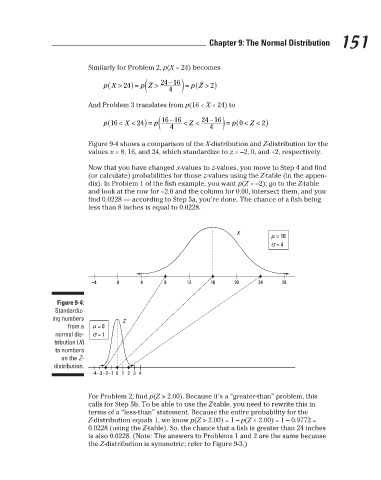
Figure 9-4 shows a comparison of the X-distribution and Z-distribution for the
values x = 8, 16, and 24, which standardize to z = –2, 0, and +2, respectively.
Now that you have changed x-values to z-values, you move to Step 4 and find
(or calculate) probabilities for those z-values using the Z-table (in the appen-
dix). In Problem 1 of the fish example, you want p(Z < –2); go to the Z-table
and look at the row for –2.0 and the column for 0.00, intersect them, and you
find 0.0228 — according to Step 5a, you’re done. The chance of a fish being
less than 8 inches is equal to 0.0228. Chapter 9: The Normal Distribution 151
X μ = 16
σ = 4
–4 0 4 8 12 16 20 24 28

Figure 9-4:
Standardiz-
ing numbers Z
from a μ = 0
normal dis- σ = 1
tribution (X)
to numbers
on the Z-
distribution.
–4 –3 –2 –1 0 1 2 3 4

For Problem 2, find p(Z > 2.00). Because it’s a “greater-than” problem, this
calls for Step 5b. To be able to use the Z-table, you need to rewrite this in
terms of a “less-than” statement. Because the entire probability for the
Z-distribution equals 1, we know p(Z > 2.00) = 1 – p(Z < 2.00) = 1 – 0.9772 =
0.0228 (using the Z-table). So, the chance that a fish is greater than 24 inches
is also 0.0228. (Note: The answers to Problems 1 and 2 are the same because
the Z-distribution is symmetric; refer to Figure 9-3.)

3/25/11 8:16 PM
15_9780470911082-ch09.indd 151 3/25/11 8:16 PM
15_9780470911082-ch09.indd 151