Page 328 - Statistics for Dummies

312
Part V: Statistical Studies and the Hunt for a Meaningful Relationship
Here’s an example to help you better understand dependence: A recent
press release put out by The Ohio State University Medical Center caught my
attention. The headline said that aspirin can prevent polyps in colon-cancer
patients. Having had a close relative who succumbed to this disease, I was
heartened at the prospect that researchers are making progress in this area
and decided to look into it.
The researchers studied 635 colon-cancer patients; they randomly assigned
approximately half of them to an aspirin regimen (317 people) and the other
half to a placebo (fake pill) regimen (318 people). They followed the patients
to see which ones developed subsequent polyps and which did not. The data
from the study are summarized in Table 19-10.
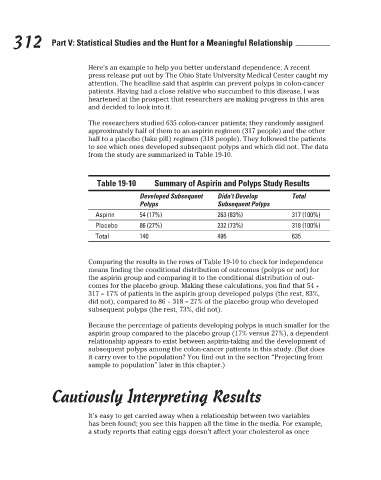
Table 19-10
Developed Subsequent
Didn’t Develop
Total
Subsequent Polyps
Polyps Summary of Aspirin and Polyps Study Results
Aspirin 54 (17%) 263 (83%) 317 (100%)
Placebo 86 (27%) 232 (73%) 318 (100%)
Total 140 495 635
Comparing the results in the rows of Table 19-10 to check for independence
means finding the conditional distribution of outcomes (polyps or not) for
the aspirin group and comparing it to the conditional distribution of out-
comes for the placebo group. Making these calculations, you find that 54 ÷
317 = 17% of patients in the aspirin group developed polyps (the rest, 83%,
did not), compared to 86 ÷ 318 = 27% of the placebo group who developed
subsequent polyps (the rest, 73%, did not).
Because the percentage of patients developing polyps is much smaller for the
aspirin group compared to the placebo group (17% versus 27%), a dependent
relationship appears to exist between aspirin-taking and the development of
subsequent polyps among the colon-cancer patients in this study. (But does
it carry over to the population? You find out in the section “Projecting from
sample to population” later in this chapter.)
Cautiously Interpreting Results
It’s easy to get carried away when a relationship between two variables
has been found; you see this happen all the time in the media. For example,
a study reports that eating eggs doesn’t affect your cholesterol as once

3/25/11 8:13 PM
27_9780470911082-ch19.indd 312 3/25/11 8:13 PM
27_9780470911082-ch19.indd 312