Page 259 - Statistics for Environmental Engineers

L1592_Frame_C29 Page 263 Tuesday, December 18, 2001 2:48 PM

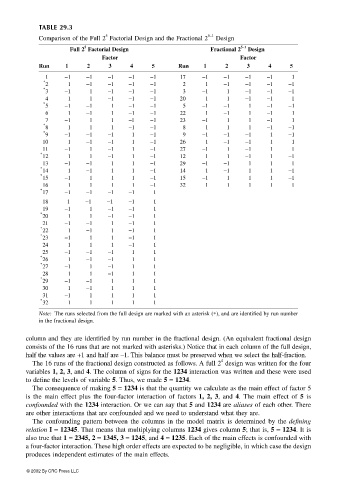
TABLE 29.3
5 5–1
Comparison of the Full 2 Factorial Design and the Fractional 2 Design
5
5–1
Full 2 Factorial Design Fractional 2 Design
Factor Factor
Run 1 2 3 4 5 Run 1 2 3 4 5
1 −1 −1 −1 −1 −1 17 −1 −1 −1 −1 1
*
2 1 −1 −1 −1 −1 2 1 −1 −1 −1 −1
*
3 −1 1 −1 −1 −1 3 −1 1 −1 −1 −1
4 1 1 −1 −1 −1 20 1 1 −1 −1 1
*
5 −1 −1 1 −1 −1 5 −1 −1 1 −1 −1
6 1 −1 1 −1 −1 22 1 −1 1 −1 1
7 −1 1 1 −1 −1 23 −1 1 1 −1 1
*
8 1 1 1 −1 −1 8 1 1 1 −1 −1
*
9 −1 −1 −1 1 −1 9 −1 −1 −1 1 −1
10 1 −1 −1 1 −1 26 1 −1 −1 1 1
11 −1 1 −1 1 −1 27 −1 1 −1 1 1
*
12 1 1 −1 1 −1 12 1 1 −1 1 −1
13 −1 −1 1 1 −1 29 −1 −1 1 1 1
*
14 1 −1 1 1 −1 14 1 −1 1 1 −1
*
15 −1 1 1 1 −1 15 −1 1 1 1 −1
16 1 1 1 1 −1 32 1 1 1 1 1
*
17 −1 −1 −1 −1 1
18 1 −1 −1 −1 1
19 −1 1 −1 −1 1
*
20 1 1 −1 −1 1
21 −1 −1 1 −1 1
*
22 1 −1 1 −1 1
*
23 −1 1 1 −1 1
24 1 1 1 −1 1
25 −1 −1 −1 1 1
*
26 1 −1 −1 1 1
*
27 −1 1 −1 1 1
28 1 1 −1 1 1
*
29 −1 −1 1 1 1
30 1 −1 1 1 1
31 −1 1 1 1 1
*
32 1 1 1 1 1
Note: The runs selected from the full design are marked with an asterisk (∗), and are identified by run number
in the fractional design.
column and they are identified by run number in the fractional design. (An equivalent fractional design
consists of the 16 runs that are not marked with asterisks.) Notice that in each column of the full design,
half the values are +1 and half are –1. This balance must be preserved when we select the half-fraction.
4
The 16 runs of the fractional design constructed as follows. A full 2 design was written for the four
variables 1, 2, 3, and 4. The column of signs for the 1234 interaction was written and these were used
to define the levels of variable 5. Thus, we made 5 = 1234.
The consequence of making 5 = 1234 is that the quantity we calculate as the main effect of factor 5
is the main effect plus the four-factor interaction of factors 1, 2, 3, and 4. The main effect of 5 is
confounded with the 1234 interaction. Or we can say that 5 and 1234 are aliases of each other. There
are other interactions that are confounded and we need to understand what they are.
The confounding pattern between the columns in the model matrix is determined by the defining
relation I = 12345. That means that multiplying columns 1234 gives column 5; that is, 5 = 1234. It is
also true that 1 = 2345, 2 = 1345, 3 = 1245, and 4 = 1235. Each of the main effects is confounded with
a four-factor interaction. These high order effects are expected to be negligible, in which case the design
produces independent estimates of the main effects.

© 2002 By CRC Press LLC