Page 105 - Structural Steel Designers Handbook AISC, AASHTO, AISI, ASTM, and ASCE-07 Design Standards

Brockenbrough_Ch03.qxd 9/29/05 5:05 PM Page 3.37

CONNECTIONS

CONNECTIONS 3.37

Equation (3.13) is easily applied to a single line weld, or a
group of parallel line welds, but when applied to weld groups
containing welds loaded at differing angles, such as depicted
in Fig. 3.25, its application becomes much more complex. In
such cases, deformation compatibility must also be satisfied.
Since transversely loaded welds are considerably less ductile
than longitudinally loaded welds, the transversely loaded
welds will fracture before the longitudinally loaded welds
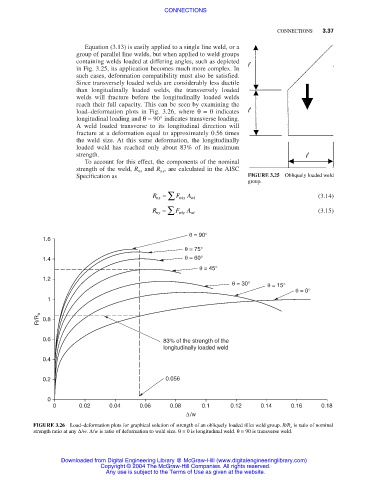
reach their full capacity. This can be seen by examining the
load–deformation plots in Fig. 3.26, where θ= 0 indicates
longitudinal loading and θ= 90° indicates transverse loading.
A weld loaded transverse to its longitudinal direction will
fracture at a deformation equal to approximately 0.56 times
the weld size. At this same deformation, the longitudinally
loaded weld has reached only about 83% of its maximum
strength.
To account for this effect, the components of the nominal
strength of the weld, R nx and R ny , are calculated in the AISC
Specification as FIGURE 3.25 Obliquely loaded weld
group.
nx ∑
R = F A wi (3.14)
wix
ny ∑
R = F A wi (3.15)
wiy

θ = 90°
1.6
θ = 75°
1.4 θ = 60°
θ = 45°
1.2
θ = 30° θ = 15°
θ = 0°
1

R/R o 0.8

0.6 83% of the strength of the
longitudinally loaded weld
0.4

0.2 0.056

0
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18
∆/w
FIGURE 3.26 Load–deformation plots for graphical solution of strength of an obliquely loaded fillet weld group. R/R o is ratio of nominal
strength ratio at any ∆/w. ∆/w is ratio of deformation to weld size. θ= 0 is longitudinal weld. θ= 90 is transverse weld.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.