Page 136 - The Combined Finite-Discrete Element Method
P. 136
GENERALISATION OF CONTACT DETECTION ALGORITHMS TO 3D SPACE 119
Level 1
Level 3
y
Level 2
x
z
Level 4
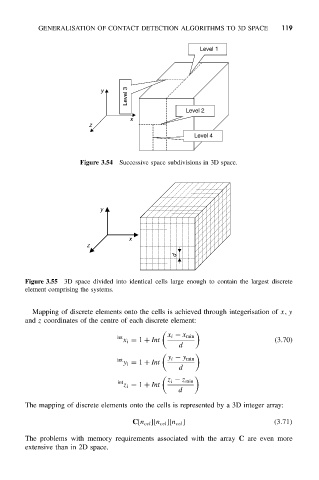
Figure 3.54 Successive space subdivisions in 3D space.
y
x
z
d
Figure 3.55 3D space divided into identical cells large enough to contain the largest discrete
element comprising the systems.
Mapping of discrete elements onto the cells is achieved through integerisation of x, y
and z coordinates of the centre of each discrete element:
int x i − x min
x i = 1 + Int (3.70)
d
int y i − y min
y i = 1 + Int
d
int z i − z min
z i = 1 + Int
d
The mapping of discrete elements onto the cells is represented by a 3D integer array:
C[n cel ][n cel ][n cel ] (3.71)
The problems with memory requirements associated with the array C are even more
extensive than in 2D space.