Page 257 - The Combined Finite-Discrete Element Method

240 TRANSITION FROM CONTINUA TO DISCONTINUA

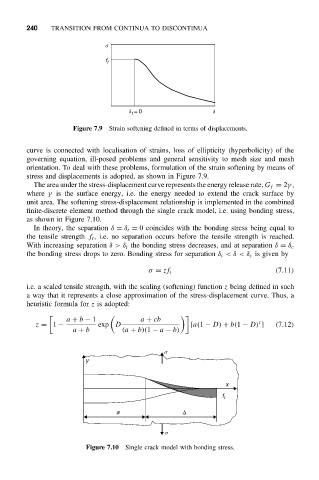
s
f t

d = 0 d
t
Figure 7.9 Strain softening defined in terms of displacements.

curve is connected with localisation of strains, loss of ellipticity (hyperbolicity) of the
governing equation, ill-posed problems and general sensitivity to mesh size and mesh
orientation. To deal with these problems, formulation of the strain softening by means of
stress and displacements is adopted, as shown in Figure 7.9.
The area under the stress-displacement curve represents the energy release rate, G f = 2γ ,
where γ is the surface energy, i.e. the energy needed to extend the crack surface by
unit area. The softening stress-displacement relationship is implemented in the combined
finite-discrete element method through the single crack model, i.e. using bonding stress,
as shown in Figure 7.10.
In theory, the separation δ = δ t = 0 coincides with the bonding stress being equal to
the tensile strength f t , i.e. no separation occurs before the tensile strength is reached.
With increasing separation δ> δ t the bonding stress decreases, and at separation δ = δ c
the bonding stress drops to zero. Bonding stress for separation δ t <δ <δ c is given by
(7.11)
σ = zf t
i.e. a scaled tensile strength, with the scaling (softening) function z being defined in such
a way that it represents a close approximation of the stress-displacement curve. Thus, a
heuristic formula for z is adopted:

a + b − 1 a + cb c

z = 1 − exp D [a(1 − D) + b(1 − D) ] (7.12)
a + b (a + b)(1 − a − b)

s
y

x
f t

a ∆

s

Figure 7.10 Single crack model with bonding stress.