Page 61 - The engineering of chemical reactions

The Batch Reactor 45

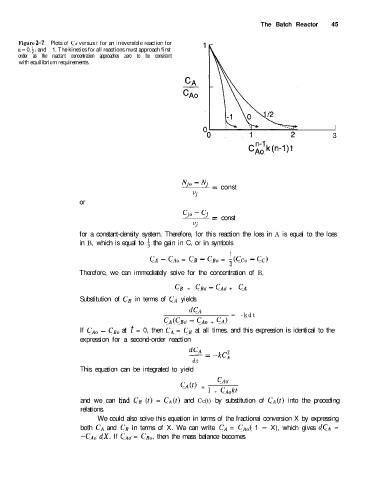
Figure 2-7 Plots of CA versus t for an irreversible reaction for
n = 0, i, and - 1. The kinetics for all reactions must approach first
order as the reactant concentration approaches zero to be consistent
with equilibrium requirements.

I
3

C;;k(n-1)t

Njo - Nj
= const
vj
or
Cjo-Cj _
- const
for a constant-density system. Therefore, for this reaction the loss in A is equal to the loss
in B, which is equal to f the gain in C, or in symbols
1
CA - CAc, = CB - c&, = -(CC, - CC)
3
Therefore, we can immediately solve for the concentration of B,

CB = CBo - CAo + CA
Substitution of CB in terms of CA yields
dC.4
= - k d t
CA(CBo - CAo + CA>
If CAM = CnO at t = 0, then CA = CB at all times, and this expression is identical to the
expression for a second-order reaction
dCA = -kc2
dt A
This equation can be integrated to yield

CA0
CA(t) =
1 + CA&t
and we can find Ce (t) = CA(t) and Cc(t) by substitution of CA(~) into the preceding
relations.
We could also solve this equation in terms of the fractional conversion X by expressing
both CA and Cn in terms of X. We can write CA = CA,,( 1 - X), which gives dCA =
-CAM dX. If CA,, = Cs,,, then the mass balance becomes