Page 1051 - The Mechatronics Handbook

36.19 Quine–McCluskey Tabular Minimization

The K-map minimization method is too cumbersome for more than six variables and does not readily
lend itself to computerization. A tabular method, which can be implemented for any number of variables
and which lends itself to computer program implementation, consists of the following steps:

1. List all the minterms in the boolean function (with their binary code) organized into groups
having the same number of 1s. The groups must be listed in consecutive order of the number of 1s.
2. Construct the list of first-order implicants. Use flags to indicate which minterms, don’t cares, or
implicants go with which functions. (Only minterms in adjacent groups have the possibility of
being adjacent and, hence, this ordering method significantly reduces the labor of compiling the
implicants.)
3. Construct the list of second-order implicants and the lists of all higher order implicants, until no
higher order implicants can be constructed.
4. Construct the prime implicant chart. The prime implicant chart shows what prime implicants
cover which minterms.
5. Select the minimum number of largest prime implicants that cover the minterms.
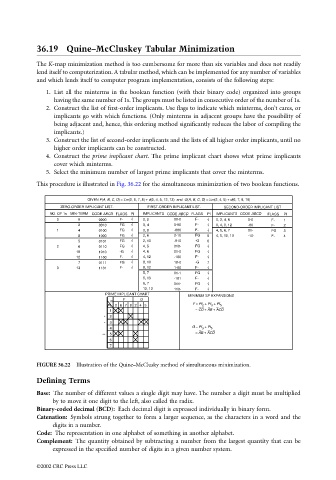
This procedure is illustrated in Fig. 36.22 for the simultaneous minimization of two boolean functions.

GIVEN F(A, B, C, D) = Σm(2, 6, 7, 8) + d(0, 4, 5, 12, 13) and G(A, B, C, D) = Σm(2, 4, 5) + d(6, 7, 8, 10)
ZERO-ORDER IMPLICANT LIST. FIRST-ORDER IMPLICANT LIST. SECOND-ORDER IMPLICANT LIST
NO. OF 1s MIN-TERM PI IMPLICANTS CODE ABCD FLAGS PI IMPLICANTS CODE ABCD FLAGS PI
CODE ABCD FLAGS
0 0 0000 F- √ 0, 2 00-0 F- √ 0, 2, 4, 6 0-0 F- 1
2 0010 FG √ 0, 4 0-00 F- √ 0, 4, 8, 12 -00 F- 2
1 4 0100 FG √ 0, 8 -000 F- √ 4, 5, 6, 7 01- FG 3
8 FG √ 2, 6 0-10 FG 5 4, 5, 12, 13 -10- F- 4
1000
5 0101 FG √ 2, 10 -010 -G 6
2 6 0110 FG √ 4, 5 010- FG √
10 1010 -G √ 4, 6 01-0 FG √
12 1100 F- √ 4, 12 -100 F- √
7 0111 FG √ 8, 10 10-0 -G 7
3 13 1101 F- √ 8, 12 1-00 F- √
5, 7 01-1 FG √
5, 13 -101 F- √
6, 7 011- FG √
12, 13 110- F- √
PRIME IMPLICANT CHART MINIMUM SP EXPANSIONS
F G
m
PI 2 6 7 8 2 4 5 F = PI 2 + PI 3 + PI 5
1 = CD + AB + ACD
* 2
* 3
4 G = PI 3 + PI 5
** 5 = AB + ACD
6
7
FIGURE 36.22 Illustration of the Quine–McClusky method of simultaneous minimization.

Defining Terms
Base: The number of different values a single digit may have. The number a digit must be multiplied
by to move it one digit to the left, also called the radix.
Binary-coded decimal (BCD): Each decimal digit is expressed individually in binary form.
Catenation: Symbols strung together to form a larger sequence, as the characters in a word and the
digits in a number.
Code: The representation in one alphabet of something in another alphabet.
Complement: The quantity obtained by subtracting a number from the largest quantity that can be
expressed in the specified number of digits in a given number system.

©2002 CRC Press LLC