Page 376 - The Mechatronics Handbook

0066_Frame_C18 Page 12 Wednesday, January 9, 2002 5:14 PM

18.17 Frequency Response

The response of any dynamic system to a sinusoidal input is called the frequency response. A generic
first-order system with a sinusoidal input of amplitude A would have the dynamic equation of
dy t() 1
------------ + -- yt() = ft() = Asin ( ωt)
dt τ
where ω is the frequency of the sinusoidal input and τ is the first-order time constant. The steady-state
solution to this equation is
yt() = AM sin ( ωt + Φ)

where M = 1/ ( τω) + 1 is the amplitude ratio (a dimensionless quantity), and Φ = −tan (τω) is the
−1
2
phase angle.
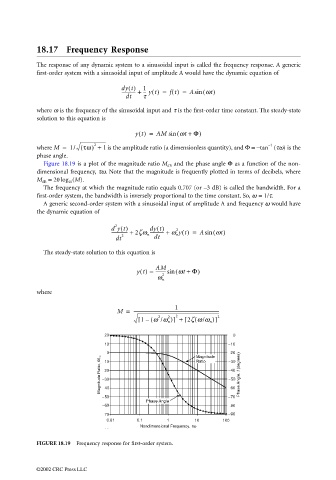
Figure 18.19 is a plot of the magnitude ratio M dB and the phase angle Φ as a function of the non-
dimensional frequency, τω. Note that the magnitude is frequently plotted in terms of decibels, where
M dB = 20 log 10 (M).
The frequency at which the magnitude ratio equals 0.707 (or –3 dB) is called the bandwidth. For a
first-order system, the bandwidth is inversely proportional to the time constant. So, ω = 1/τ.
A generic second-order system with a sinusoidal input of amplitude A and frequency ω would have
the dynamic equation of
2
d yt() dy t() ω n yt() = Asin ( ωt)
------------ +
-------------- +
2
dt 2 2ζω n dt
The steady-state solution to this equation is
yt() = AM ( ωt + Φ)
---------sin
2
ω n
where

1
M = -----------------------------------------------------------------------------
[ 1 (– ω /ω n )] + [ 2ζω/ω n )] 2
(
2
2
2

FIGURE 18.19 Frequency response for first-order system.

©2002 CRC Press LLC