Page 46 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

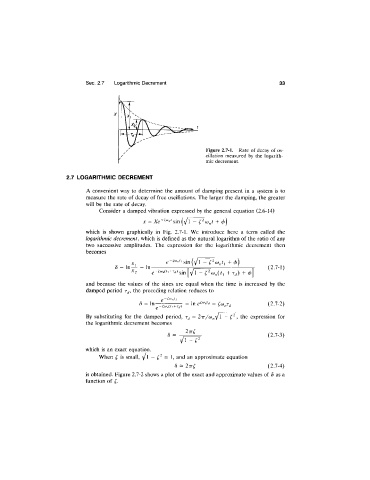
Sec. 2.7 Logarithmic Decrement 33

Figure 2.7-1. Rate of decay of os­
cillation measured by the logarith­
mic decrement.

2.7 LOGARITHMIC DECREMENT

A convenient way to determine the amount of damping present in a system is to
measure the rate of decay of free oscillations. The larger the damping, the greater
will be the rate of decay.
Consider a damped vibration expressed by the general equation (2.6-14)
= A'e-f“’"' sin (v/l -
which is shown graphically in Fig. 2.7-1. We introduce here a term called the
logarithmic decrement, which is defined as the natural logarithm of the ratio of any
two successive amplitudes. The expression for the logarithmic decrement then
becomes

sin (^1 - + <{> )
8 = In-^ = In- (2.7-1)
sin + Trf) + </.]
and because the values of the sines are equal when the time is increased by the
damped period the preceding relation reduces to

Ô= In- = In = C^n'^d (2.7-2)
By substituting for the damped period, 1 — , the expression for
the logarithmic decrement becomes
2ir^
8 = (2.7-3)

which is an exact equation.
When is small, ^/l — = 1, and an approximate equation
8 = 2tt£ (2.7-4)
is obtained. Figure 2.7-2 shows a plot of the exact and approximate values of 5 as a
function of