Page 47 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

34 Free Vibration Chap. 2

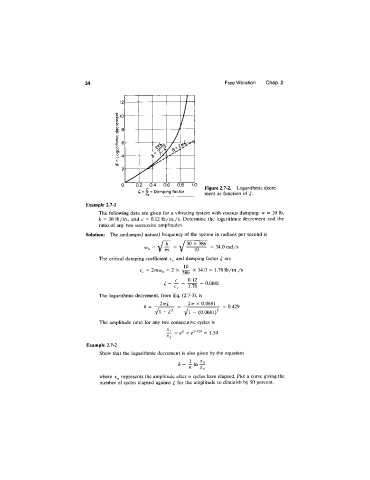
Figure 2.7-2. Logarithmic decre­
ment as function of
Example 2.7-1
The following data are given for a vibrating system with viscous damping: w = 10 lb,
:
A = 30 Ib/in., and c = 0.12 Ib/in./s. Determine the logarithmic decrement and the
ratio of any two successive amplitudes.
Solution: The undamped natural frequency of the system in radians per second is
p i / 30 X 386 ^ ,
V m ^ V ----^ 10
The critical damping coefficient and damping factor ( are

= 2mo)^ == 2 X X 34.0 = 1.76 Ib/in./s
c. " 1.76
The logarithmic decrement, from Eq. (2.7-3), is
2ttì 2v X 0.0681
8 = 0.429
V^l - (0.0681)^
The amplitude ratio for any two consecutive cycles is
JIC i

Example 2.7-2
Show that the logarithmic decrement is also given by the equation
1 -^n
5 = - In —
n x„
where represents the amplitude after n cycles have elapsed. Plot a curve giving the
number of cycles elapsed against ^ for the amplitude to diminish by 50 percent.