Page 48 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

Sec. 2.8 Coulomb Damping 35

Solution: The amplitude ratio for any two consecutive amplitudes is
Xi X2 ^3
The ratio can be written as
Í! -(Í7)(S)(Íí)
from which the required equation is obtained as
8 - i l n S
n x^
To determine the number of cycles elapsed for a 50-percent reduction in
amplitude, we obtain the following relation from the preceding equation:

_
0.693
. ^
1 , .
b = l i r i = — In 2 = --------
^ n n
= 0 ^ = 0.110
277
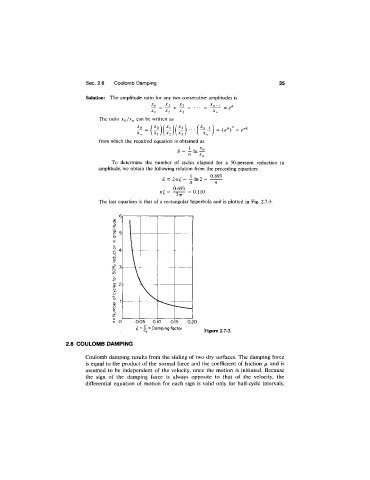
The last equation is that of a rectangular hyperbola and is plotted in Fig. 2.7-3.

Figure 2.7-3.
2.8 COULOMB DAMPING

Coulomb damping results from the sliding of two dry surfaces. The damping force
is equal to the product of the normal force and the coefficient of friction fx and is
assumed to be independent of the velocity, once the motion is initiated. Because
the sign of the damping force is always opposite to that of the velocity, the
differential equation of motion for each sign is valid only for half-cycle intervals.