Page 488 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

Sec. 14.6 Method of Iteration 475

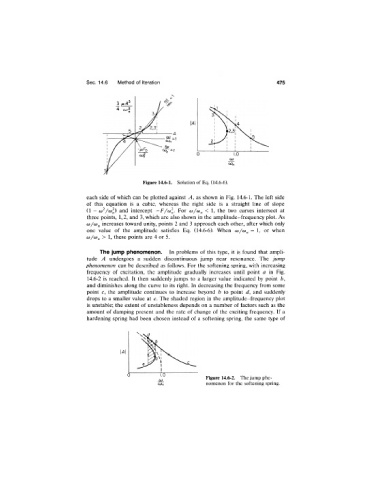
Figure 14.6-1. Solution of Eq. (14.6-6).

each side of which can be plotted against A, as shown in Fig. 14.6-1. The left side
of this equation is a cubic, whereas the right side is a straight line of slope
(1 - ù)^/(ol) and intercept -F/w ^. For ù)/(o^ < 1, the two curves intersect at
three points, 1,2, and 3, which are also shown in the amplitude-frequency plot. As
(o/ct>„ increases toward unity, points 2 and 3 approach each other, after which only
one value of the amplitude satisfies Eq. (14.6-6). When co/co^ = 1, or when
(o/co^ > 1, these points are 4 or 5.

The jump phenomenon. In problems of this type, it is found that ampli­
tude A undergoes a sudden discontinuous jump near resonance. The jump
phenomenon can be described as follows. For the softening spring, with increasing
frequency of excitation, the amplitude gradually increases until point a in Fig.
14.6-2 is reached. It then suddenly jumps to a larger value indicated by point b,
and diminishes along the curve to its right. In decreasing the frequency from some
point c, the amplitude continues to increase beyond b to point d, and suddenly
drops to a smaller value at e. The shaded region in the amplitude-frequency plot
is unstable; the extent of unstableness depends on a number of factors such as the
amount of damping present and the rate of change of the exciting frequency. If a
hardening spring had been chosen instead of a softening spring, the same type of

Figure 14.6-2. The jump phe­
OJn nomenon for the softening spring.