Page 306 - Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

276 Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

where k is the turbulent kinetic energy, υ t is the eddy viscosity (and can be
2
defined as C μ k /ε), Pr t is the turbulent Prandtl number, and ε is the turbulent
kinetic energy dissipation rate. To get a better understanding of some specific
problems that occur in the modeling of the turbulent heat flux for low Prandtl
fluids, some peculiarities related to the problem are summarized in the following
sections.

6.2.1.1.1 Incomplete modeling of turbulent heat flux
The definition of the heat flux, as given in the Eq. (6.2.1.4), implies that the com-
ponents of the turbulent heat flux are aligned with the corresponding components
of the temperature gradient vector. This assumption eventually leads to the model
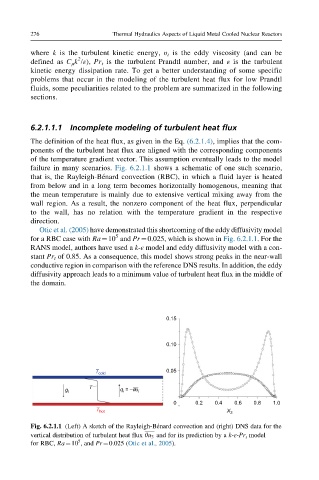
failureinmanyscenarios. Fig. 6.2.1.1 shows a schematic of one such scenario,
that is, the Rayleigh-B enard convection (RBC), in which a fluid layer is heated
from below and in a long term becomes horizontally homogenous, meaning that
the mean temperature is mainly due to extensive vertical mixing away from the
wall region. As a result, the nonzero component of the heat flux, perpendicular
to the wall, has no relation with the temperature gradient in the respective
direction.
Otic et al. (2005) have demonstrated this shortcoming of the eddy diffusivity model
5
for a RBC case with Ra¼10 and Pr¼0.025, which is shown in Fig. 6.2.1.1. For the
RANS model, authors have used a k-ε model and eddy diffusivity model with a con-
stant Pr t of 0.85. As a consequence, this model shows strong peaks in the near-wall
conductive region in comparison with the reference DNS results. In addition, the eddy
diffusivity approach leads to a minimum value of turbulent heat flux in the middle of
the domain.

0.15

0.10

0.05
T cold
T
g i q i = –qu i
0 0.2 0.4 0.6 0.8 1.0
T hot
X 3
Fig. 6.2.1.1 (Left) A sketch of the Rayleigh-B enard convection and (right) DNS data for the
vertical distribution of turbulent heat flux θu 3 and for its prediction by a k-ε-Pr t model
5
for RBC, Ra¼10 , and Pr¼0.025 (Otic et al., 2005).