Page 308 - Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

278 Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

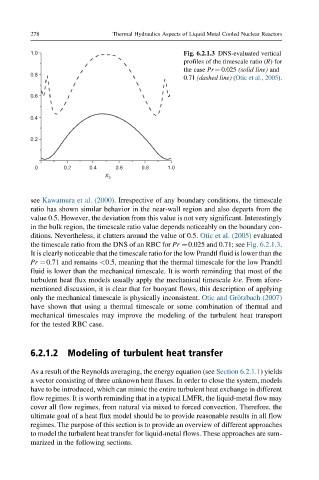
1.0 Fig. 6.2.1.3 DNS-evaluated vertical
profiles of the timescale ratio (R) for
the case Pr¼ 0.025 (solid line) and
0.8
0.71 (dashed line) (Otic et al., 2005).

0.6

0.4

0.2

0 0.2 0.4 0.6 0.8 1.0
X 3

see Kawamura et al. (2000). Irrespective of any boundary conditions, the timescale
ratio has shown similar behavior in the near-wall region and also departs from the
value 0.5. However, the deviation from this value is not very significant. Interestingly
in the bulk region, the timescale ratio value depends noticeably on the boundary con-
ditions. Nevertheless, it clutters around the value of 0.5. Otic et al. (2005) evaluated
the timescale ratio from the DNS of an RBC for Pr ¼0.025 and 0.71; see Fig. 6.2.1.3.
It is clearly noticeable that the timescale ratio for the low Prandtl fluid is lower than the
Pr ¼0.71 and remains <0.5, meaning that the thermal timescale for the low Prandtl
fluid is lower than the mechanical timescale. It is worth reminding that most of the
turbulent heat flux models usually apply the mechanical timescale k/ε. From afore-
mentioned discussion, it is clear that for buoyant flows, this description of applying
only the mechanical timescale is physically inconsistent. Otic and Gr€ otzbach (2007)
have shown that using a thermal timescale or some combination of thermal and
mechanical timescales may improve the modeling of the turbulent heat transport
for the tested RBC case.

6.2.1.2 Modeling of turbulent heat transfer

As a result of the Reynolds averaging, the energy equation (see Section 6.2.1.1) yields
a vector consisting of three unknown heat fluxes. In order to close the system, models
have to be introduced, which can mimic the entire turbulent heat exchange in different
flow regimes. It is worth reminding that in a typical LMFR, the liquid-metal flow may
cover all flow regimes, from natural via mixed to forced convection. Therefore, the
ultimate goal of a heat flux model should be to provide reasonable results in all flow
regimes. The purpose of this section is to provide an overview of different approaches
to model the turbulent heat transfer for liquid-metal flows. These approaches are sum-
marized in the following sections.