Page 313 - Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

Turbulent heat transport 283

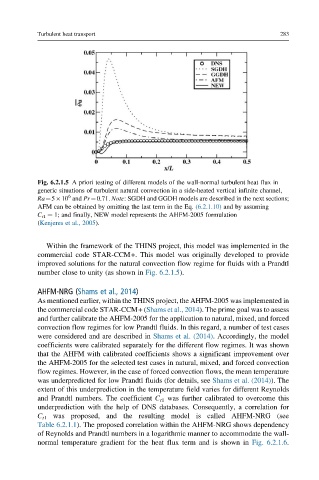
Fig. 6.2.1.5 A priori testing of different models of the wall-normal turbulent heat flux in
generic situations of turbulent natural convection in a side-heated vertical infinite channel,
6
Ra¼5 10 and Pr¼0.71. Note: SGDH and GGDH models are described in the next sections;
AFM can be obtained by omitting the last term in the Eq. (6.2.1.10) and by assuming
C t1 ¼ 1; and finally, NEW model represents the AHFM-2005 formulation
(Kenjeres et al., 2005).

Within the framework of the THINS project, this model was implemented in the
commercial code STAR-CCM+. This model was originally developed to provide
improved solutions for the natural convection flow regime for fluids with a Prandtl
number close to unity (as shown in Fig. 6.2.1.5).

AHFM-NRG (Shams et al., 2014)
As mentioned earlier, within the THINS project, the AHFM-2005 was implemented in
the commercial code STAR-CCM+ (Shams et al., 2014). The prime goal was to assess
and further calibrate the AHFM-2005 for the application to natural, mixed, and forced
convection flow regimes for low Prandtl fluids. In this regard, a number of test cases
were considered and are described in Shams et al. (2014). Accordingly, the model
coefficients were calibrated separately for the different flow regimes. It was shown
that the AHFM with calibrated coefficients shows a significant improvement over
the AHFM-2005 for the selected test cases in natural, mixed, and forced convection
flow regimes. However, in the case of forced convection flows, the mean temperature
was underpredicted for low Prandtl fluids (for details, see Shams et al. (2014)). The
extent of this underprediction in the temperature field varies for different Reynolds
and Prandtl numbers. The coefficient C t1 was further calibrated to overcome this
underprediction with the help of DNS databases. Consequently, a correlation for
C t1 was proposed, and the resulting model is called AHFM-NRG (see
Table 6.2.1.1). The proposed correlation within the AHFM-NRG shows dependency
of Reynolds and Prandtl numbers in a logarithmic manner to accommodate the wall-
normal temperature gradient for the heat flux term and is shown in Fig. 6.2.1.6.