Page 318 - Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

288 Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

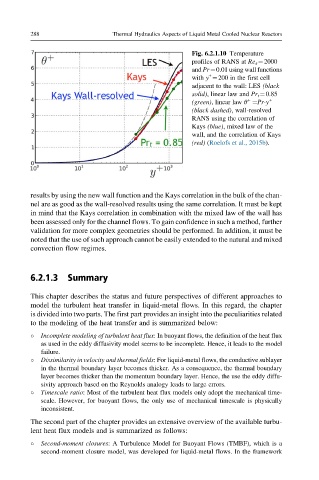
Fig. 6.2.1.10 Temperature
profiles of RANS at Re τ ¼2000
and Pr¼0.01 using wall functions
+
with y ¼200 in the first cell
adjacent to the wall: LES (black
solid), linear law and Pr t ¼0.85
+
(green), linear law θ ¼Pr y +
(black dashed), wall-resolved
RANS using the correlation of
Kays (blue), mixed law of the
wall, and the correlation of Kays
(red) (Roelofs et al., 2015b).

results by using the new wall function and the Kays correlation in the bulk of the chan-
nel are as good as the wall-resolved results using the same correlation. It must be kept
in mind that the Kays correlation in combination with the mixed law of the wall has
been assessed only for the channel flows. To gain confidence in such a method, further
validation for more complex geometries should be performed. In addition, it must be
noted that the use of such approach cannot be easily extended to the natural and mixed
convection flow regimes.

6.2.1.3 Summary

This chapter describes the status and future perspectives of different approaches to
model the turbulent heat transfer in liquid-metal flows. In this regard, the chapter
is divided into two parts. The first part provides an insight into the peculiarities related
to the modeling of the heat transfer and is summarized below:
Incomplete modeling of turbulent heat flux: In buoyant flows, the definition of the heat flux
as used in the eddy diffusivity model seems to be incomplete. Hence, it leads to the model
failure.
Dissimilarity in velocity and thermal fields: For liquid-metal flows, the conductive sublayer
in the thermal boundary layer becomes thicker. As a consequence, the thermal boundary
layer becomes thicker than the momentum boundary layer. Hence, the use the eddy diffu-
sivity approach based on the Reynolds analogy leads to large errors.
Timescale ratio: Most of the turbulent heat flux models only adopt the mechanical time-
scale. However, for buoyant flows, the only use of mechanical timescale is physically
inconsistent.

The second part of the chapter provides an extensive overview of the available turbu-
lent heat flux models and is summarized as follows:

Second-moment closures: A Turbulence Model for Buoyant Flows (TMBF), which is a
second-moment closure model, was developed for liquid-metal flows. In the framework