Page 316 - Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

286 Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear Reactors

This GGDH formulation represents a nonisotropic eddy diffusivity model and, hence,
shows better prediction of the turbulent heat flux in comparison with an isotropic eddy
diffusivity model, as shown in Fig. 6.2.1.5.

6.2.1.2.4 Simple gradient diffusion hypothesis
Replacing the turbulence stress u i u j in the Eq. (6.2.1.11) by its trace u i u i ¼ 2k leads to
the standard isotropic eddy diffusivity model, also known as the simple gradient dif-
fusion hypothesis (SGDH). This is the most widely used approach to compute the tur-
bulent heat fluxes and is based on the Reynolds analogy. The method uses the concept
of the turbulent Prandtl number and is available in almost all the CFD codes. There
have been a number of studies, which give a good insight into the behavior of Pr t .
However, these studies are mostly limited to simple flow configurations and a few
working fluids, for example, Gr€ otzbach (2007). Based on the available knowledge,
the approach of using Pr t , either a constant value or in the form of a correlation,
has been adopted in several ways to evaluate turbulent heat transfer. Most of the
CFD codes, by default, use a constant value of Pr t ¼0.85 or 0.9. However, this leads
to a series of shortcomings (also highlighted in Section 6.2.1.1). It is well known that
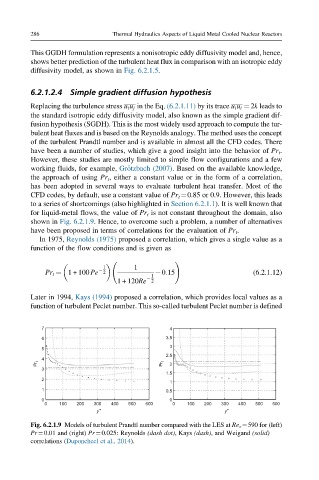
for liquid-metal flows, the value of Pr t is not constant throughout the domain, also
shown in Fig. 6.2.1.9. Hence, to overcome such a problem, a number of alternatives
have been proposed in terms of correlations for the evaluation of Pr t .
In 1975, Reynolds (1975) proposed a correlation, which gives a single value as a
function of the flow conditions and is given as

!

1 1

Pr t ¼ 1 + 100 Pe 2 0:15 (6.2.1.12)
1

1 + 120Re 2
Later in 1994, Kays (1994) proposed a correlation, which provides local values as a
function of turbulent Peclet number. This so-called turbulent Peclet number is defined
7 4
6 3.5
3
5
2.5
4
Pr t Pr t 2
3
1.5
2
1
1 0.5
0 0
0 100 200 300 400 500 600 0 100 200 300 400 500 600
y + y +
Fig. 6.2.1.9 Models of turbulent Prandtl number compared with the LES at Re τ ¼590 for (left)
Pr¼0.01 and (right) Pr¼0.025: Reynolds (dash dot), Kays (dash), and Weigand (solid)
correlations (Duponcheel et al., 2014).