Page 119 - Thermodynamics of Biochemical Reactions

6.6 Consideration of Glycolysis 115

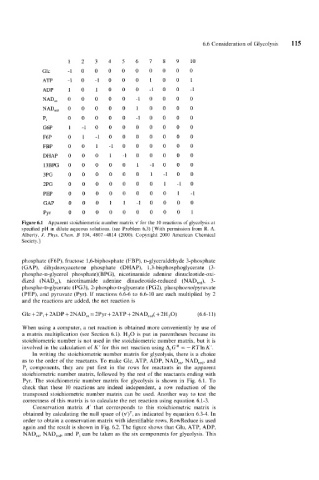
1 2 3 4 5 6 7 8 9 10
Glc -1 0 0 0 0 0 0 0 0 0

ATP - 1 0 - 1 0 0 0 1 0 0 1
ADP 1 0 1 0 0 0 -1 0 0 -1
NAD,, 0 0 0 0 0 -I 0 0 0 0
NAD,,O 0 0 0 0 1 0 0 0 0
p, 0 0 0 0 0 -1 0 0 0 0
G6P 1-1 0 0 0 0 0 0 0 0
F6P 0 1-1 0 0 0 0 0 0 0
FBP 0 0 1 - 1 0 0 0 0 0 0
DHAP 0 0 0 1 - 1 0 0 0 0 0
13BPG 0 0 0 0 0 1 -I 0 0 0

3PG 0 0 0 0 0 0 1-1 0 0
2PG 0 0 0 0 0 0 0 1-1 0
PEP 0 0 0 0 0 0 0 0 1 - 1
GAP 0 0 0 1 1 - 1 0 0 0 0
PYr 0 0 0 0 0 0 0 0 0 1

Figure 6.1 Apparent stoichiometric number matrix v’ for the 10 reactions of glycolysis at
specified pH in dilute aqueous solutions. (see Problem 6.3) [With permission from R. A.
Alberty, J. Phys. Ckrm. B 104, 4807-4814 (2000). Copyright 2000 American Chemical
Society.]

phosphate (F6P), fructose 1,6-biphosphate (FBP), D-glyceraldehyde 3-phosphate
(GAP), dihydroxyacetone phosphate (DHAP), 1,3-bisphosphoglycerate (3-
phospho-D-glycerol phosphate)(BPG), nicotinamide adenine dinucleotide-oxi-
dized (NAD,,), nicotinamide adenine dinucleotide-reduced (NAD,,,), 3-
phospho-D-glycerate (PG3), 2-phospho-~-glycerate (PG2), phosphoenolpyruvate
(PEP), and pyruvate (Pyr). If reactions 6.6-6 to 6.6-10 are each multiplied by 2
and the reactions are added. the net reaction is

Glc + 2P, + 2ADP + 2NAD,, = 2Pyr + 2ATP + 2NAD,,,( + 2H,O) (6.6-11)

When using a computer, a net reaction is obtained more conveniently by use of
a matrix multiplication (see Section 6.1). H,O is put in parentheses because its
stoichiometric number is not used in the stoichiometric number matrix, but it is
involved in the calculation of K’ for this net reaction using A,G” = - RTlnK’.
In writing the stoichiometric number matrix for glycolysis, there is a choice
as to the order of the reactants. To make Glc, ATP, ADP, NAD,,, NAD,,,, and
P, components, they are put first in the rows for reactants in the apparent
stoichiometric number matrix, followed by the rest of the reactants ending with
Pyr. The stoichiometric number matrix for glycolysis is shown in Fig. 6.1. To
check that these 10 reactions are indeed independent, a row reduction of the
transposed stoichiometric number matrix can be used. Another way to test the
correctness of this matrix is to calculate the net reaction using equation 6.1-3.
Conservation matrix A’ that corresponds to this stoichiometric matrix is
obtained by calculating the null space of (v’)~, as indicated by equation 6.3-4. In
order to obtain a conservation matrix with identifiable rows, RowReduce is used
again and the result is shown in Fig. 6.2. The figure shows that Glu, ATP, ADP,
NAD,,, NAD,,,, and PI can be taken as the six components for glycolysis. This