Page 242 - Thermodynamics of Biochemical Reactions

Mathematica Solutions to Problems

klATP = 3.43*10"-7;
k2ATP .000140;
k3ATP= .000123;
k4ATP=.0118;
kSATP= .0279;
klADP=4.70*10"-7;
k2ADP= .000161;
k3ADP = -00113;
k4ADP= .0431;
klP= 2.24*10"-7;
k2P= .0266;
kre€= .222;
pATP= 1+ (lOA-pH) /klATP+ (10" (-2*pH)) / (klATP*k2ATP) + (lOA-pMg) /k3ATP+
((10"-pH) * (lO"-pMg)) / (klATP*kIATP) + (10" (-2*pMg)) / (k3ATP*kSATP);
pADP= 1+ (lO"-pH) /klADP+ (10" (-2*pH)) / (klADP*k2ADP) +
(lOA-pMg) /k3ADP+ ( (lOA-pH) * (10"-pMg)) / (klADP*kIADP);
pP = 1 + (10 A -pH) / klP + (10 A -pMg) / k2P;
kapp = kref * pADP * pP / ( (10 -pH) * pATP) ;

nHrx= -D[Log[kapp], pH] /Log[lO];
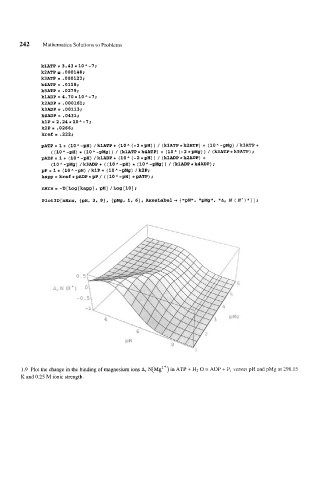
Plot3D[nHrx, {pH, 3, 9}, {pMg, 1, 6}, AxesLabel + {"pH", "pMg", "Ar N (If')"}];

1.9 Plot the change in the binding of magnesium ions Ar N(Mg2+) in ATP + H2 0 = ADP + P, versus pH and pMg at 298.15
K and 0.25 M ionic strength.