Page 340 - Thermodynamics of Biochemical Reactions

340 Mathematica Solutions to Problems

kT2=1.221*10"4;

kT3=4.049*10"5;

kT4=6.644*10"5;

yT=(kT1*o2+2*kT1*kT2*o2"2+3*kTl*kT2*kT3*o2A3+4*kTl*kT2*kT3*kT4*o2A4)/(4*(l+kTl*o2+kTl*k
);
T2*02*2+kTl*kT2*kT3*02"3+kT1*kTl*kT2*kT3*kT4*02~4)

1

0.8-

0.6-

0.4-

0.2-

'0 .'OoOOl5' ' 0. OOO06°2
5~10-~ 0.00001 '

Plot[Evaluate[o2*D[Log[pT]/4,o2ll,{o2,lOA-8,2*lOA-5~,PlotRange-~~O,l~,~eS~ab~~-
1
>( [\ ! \ (0\-2\) ", 'I\ ! \ (Y\-T\) "11 i

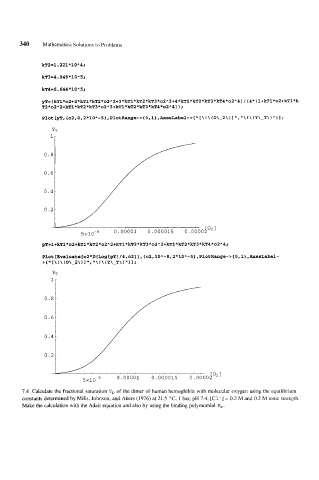
7.4 Calculate the fractional saturation Y, of the dimer of human hemoglobin with molecular oxygen using the equilibrium
constants determined by Mills, Johnson, and Akers (1976) at 21.5 OC, 1 bar, pH 7.4, [Cl-] = 0.2 M and 0.2 M ionic strength.
Make the calculation with the Adair equation and also by using the binding polymomial P, .