Page 342 - Thermodynamics of Biochemical Reactions

342 Mathematica Solutions to Problems

(a) The values of Y, and Y, are calclted as follows:

kT1=4.397*10"4;

kT2=1.221*10"4;

kT3=4.049*10"5;
kT4=6.644*10"5;

kD1=3.253*10"6;

kD2=8.155*10"5;

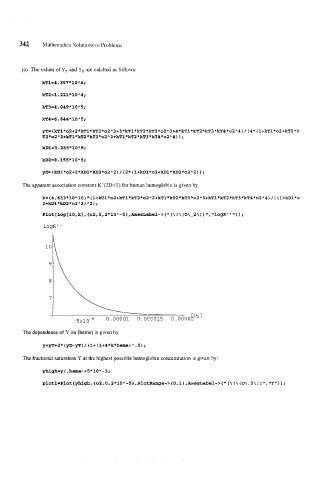
The apparent association constant K"(2D=T) for human hemoglobin is given by

k=(4.633*10"10)*(l+kTl*o2+kTl*kT2*o2A2+kTl*kT2*kT3*o2A3+kTl*kT2*kT3*kT4*o2A4)/( (l+kDl*o
2+kDl*kD2*02"2)"2);
I' 11;
plot [Log [ 10, k] , {02,0,2 * 10 A - 5 1 , AxesLabel - > { 1 \ ! \ ( O\-2 \ ) 1 'I, logK I

The dependence of Y on [heme] is given by

The fractional saturation Y at the highest possible hemoglobin concentration is given by:

yhigh=y/.hme->5*lOA-3;

plotlaplot [yhigh, {02, 0,2*1OA-5),PlotRange->{O, 1) ,AxesLabel->{" [\! \ (0\-2\) I ", "Y"1 1 ;