Page 319 - Bird R.B. Transport phenomena

§10.6 Heat Conduction Through Composite Walls 303

Zone II in which heat
is produced by
Zone I chemical reaction Zone III
10
N = 2

N = 1
a,
6,=1
N='-1
'с I
.о h. N = -2
ел ' w 0.1 -
С II N/
в ~e

0.01 1 t i l l
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1.0 1.2
Dimensionless axial coordinate Z = z/L
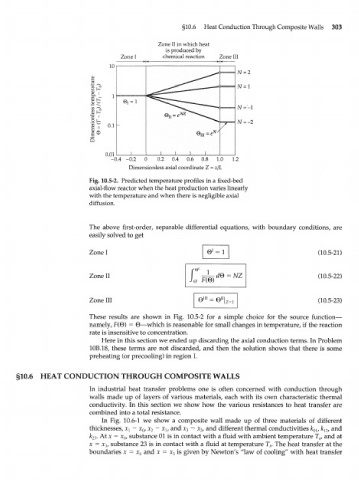
Fig. 10.5-2. Predicted temperature profiles in a fixed-bed
axial-flow reactor when the heat production varies linearly
with the temperature and when there is negligible axial
diffusion.

The above first-order, separable differential equations, with boundary conditions, are
easily solved to get

Zone I (10.5-21)

Zone II (10.5-22)

11
Zone III е ш = е Z=l (10.5-23)

These results are shown in Fig. 10.5-2 for a simple choice for the source function—
namely, F(©) = В—which is reasonable for small changes in temperature, if the reaction
rate is insensitive to concentration.
Here in this section we ended up discarding the axial conduction terms. In Problem
10B.18, these terms are not discarded, and then the solution shows that there is some
preheating (or precooling) in region I.

§10.6 HEAT CONDUCTION THROUGH COMPOSITE WALLS

In industrial heat transfer problems one is often concerned with conduction through
walls made up of layers of various materials, each with its own characteristic thermal
conductivity. In this section we show how the various resistances to heat transfer are
combined into a total resistance.
In Fig. 10.6-1 we show a composite wall made up of three materials of different
thicknesses, x } - x , x 2 - x b and x 3 - x , and different thermal conductivities fc k , and
01/
2
u
0
k . At x = x , substance 01 is in contact with a fluid with ambient temperature T , and at
2?>
a
()
x = x , substance 23 is in contact with a fluid at temperature T . The heat transfer at the
b
3
boundaries x = x and x = x is given by Newton's "law of cooling" with heat transfer
{) 3