Page 345 - Bird R.B. Transport phenomena

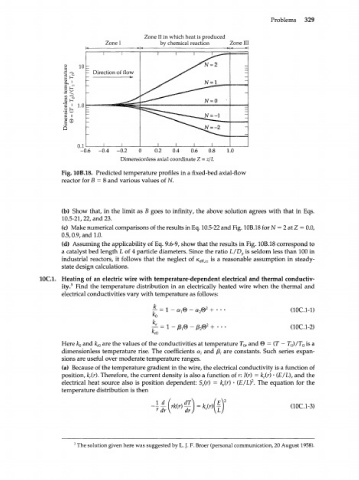
Problems 329

Zone II in which heat is produced
Zone I by chemical reaction Zone III

1 1 |
10 =
- Direction of flow i и i
Eh? I и
I
I
1.0 ~ I
il
ел 11 1 1 1
С 1 I
1 I I
I
I
О 1 I I
0.1 I I I I
-0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1.0
Dimensionless axial coordinate Z = z/L
Fig. 10ВЛ8. Predicted temperature profiles in a fixed-bed axial-flow
reactor for В = 8 and various values of N.

(b) Show that, in the limit as В goes to infinity, the above solution agrees with that in Eqs.
10.5-21,22, and 23.
(c) Make numerical comparisons of the results in Eq. 10.5-22 and Fig. 10B.18 for N = 2 at Z = 0.0,
0.5,0.9, and 1.0.
(d) Assuming the applicability of Eq. 9.6-9, show that the results in Fig. 10B.18 correspond to
a catalyst bed length L of 4 particle diameters. Since the ratio L/D is seldom less than 100 in
p
industrial reactors, it follows that the neglect of K is a reasonable assumption in steady-
effzz
state design calculations.
10C.1. Heating of an electric wire with temperature-dependent electrical and thermal conductiv-
ity. 3 Find the temperature distribution in an electrically heated wire when the thermal and
electrical conductivities vary with temperature as follows:

£ = !-, - а в 2 + (lOC.1-1)
2
- /3 0 2 (lOC.1-2)
2
Here k and k are the values of the conductivities at temperature T , and 0 = (Г - T )/T is a
0 e0 o o o
dimensionless temperature rise. The coefficients a { and Д are constants. Such series expan-
sions are useful over moderate temperature ranges.
(a) Because of the temperature gradient in the wire, the electrical conductivity is a function of
position, k (r). Therefore, the current density is also a function of r: I(r) = k (r) • (£/L), and the
c e
2
electrical heat source also is position dependent: S e(r) = k e(r) • (E/L) . The equation for the
temperature distribution is then
(lOC.1-3)

3
The solution given here was suggested by L. J. F. Broer (personal communication, 20 August 1958).