Page 636 - Bird R.B. Transport phenomena

616 Chapter 20 Concentration Distributions with More Than One Independent Variable

1.0

0.8
1 Э- \ \
N s_ N N ч
-err( + 0.6 \ Ч

i к = 1 - 1^ <^ ч 3 /4
0.4 1 11-
н
1 П
X 0.2 XА0 = N.
-
0 ==
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0

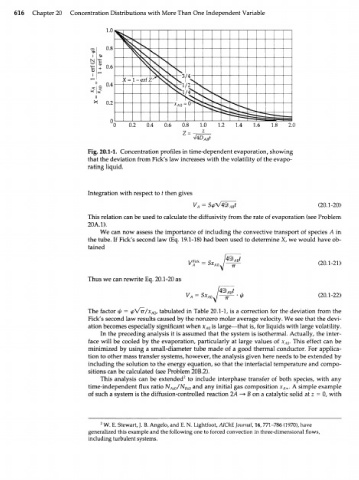
Fig. 20.1-1. Concentration profiles in time-dependent evaporation, showing
that the deviation from Fick's law increases with the volatility of the evapo-
rating liquid.

Integration with respect to t then gives
(20.1-20)
This relation can be used to calculate the diffusivity from the rate of evaporation (see Problem
20A.1).
We can now assess the importance of including the convective transport of species Л in
the tube. If Fick's second law (Eq. 19.1-18) had been used to determine X, we would have ob-
tained

V / ¥ k = Sx (20.1-21)

Thus we can rewrite Eq. 20.1-20 as

(20.1-22)

The factor ф = <рЛ/тг/х , tabulated in Table 20.1-1, is a correction for the deviation from the
А0
Fick's second law results caused by the nonzero molar average velocity. We see that the devi-
ation becomes especially significant when x A0 is large—that is, for liquids with large volatility.
In the preceding analysis it is assumed that the system is isothermal. Actually, the inter-
face will be cooled by the evaporation, particularly at large values of х . This effect can be
ло
minimized by using a small-diameter tube made of a good thermal conductor. For applica-
tion to other mass transfer systems, however, the analysis given here needs to be extended by
including the solution to the energy equation, so that the interfacial temperature and compo-
sitions can be calculated (see Problem 20B.2).
This analysis can be extended 2 to include interphase transfer of both species, with any
time-independent flux ratio N /N Bz0 and any initial gas composition х . A simple example
Лх
Az0
of such a system is the diffusion-controlled reaction 2Л —> В on a catalytic solid at z = 0, with

2 W. E. Stewart, J. B. Angelo, and E. N. Lightfoot, AIChE journal, 16, 771-786 (1970), have
generalized this example and the following one to forced convection in three-dimensional flows,
including turbulent systems.