Page 50 - Water Engineering Hydraulics, Distribution and Treatment

28
Water Sources: Surface Water
Chapter 2
EXAMPLE 2.2 DESIGN OF STORAGE REQUIREMENT FOR VARIOUS FREQUENCIES
Examination of the 25-year record of runoff from an eastern stream shows that the storage amounts listed in Table 2.3 are needed
2
in successive years to maintain a draft of 750,000 gpd/mi (1,096,000 L/d/km ). Estimate the design storage requirement that is
probably reached or exceeded but once in 20, 50, and 100 years.
Table 2.3
Storage requirements (Example 2.2)
7
6
1
3
4
2
Order of year
104
37
39
29
Calculated storage (MG)
47
78
74
82
110
22
15
25
20
21
14
19
Order of year
23
24
16
17
18
51
8
88
Calculated storage (MG)
65
61
20
72
10
73
117
53
Conversion factors: 1 MG = 1,000,000 gal = 3.785 ML = 3,785,000 L. 115 5 35 2 102 81 8 124 9 10 11 12 13
Solution:
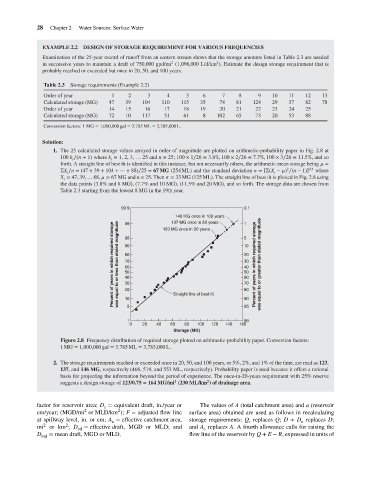
1. The 25 calculated storage values arrayed in order of magnitude are plotted on arithmetic-probability paper in Fig. 2.8 at
100 k ∕(n + 1) where k = 1, 2, 3, … 25 and n = 25; 100 × 1∕26 = 3.8%, 100 × 2∕26 = 7.7%, 100 × 3∕26 = 11.5%,andso
i
i
forth. A straight line of best fit is identified in this instance, but not necessarily others, the arithmetic mean storage being =
2
ΣX ∕n = (47 + 39 + 104 + ⋯ + 88)∕25 = 67 MG (254 ML) and the standard deviation = [Σ(X − ) ∕(n − 1)] 0.5 where
i
i
X = 47, 39, … 88, = 67 MG and n = 25. Then = 33 MG (125 ML). The straight line of best fit is plotted in Fig. 2.8 using
i
the data points (3.8% and 8 MG), (7.7% and 10 MG), (11.5% and 20 MG), and so forth. The storage data are chosen from
Table 2.3 starting from the lowest 8 MG in the 19th year.
99.9 0.1
146 MG once in 100 years 1 5
137 MG once in 50 years
99
Percent of years in which required storage was equal to or less than stated magnitude 90 10 Percent of years in which required storage was equal to or greater than stated magnitude
123 MG once in 20 years
95
20
80
70
30
60
40
50
50
40
60
70
30
80
20
10
95
1 5 Straight line of best fit 90
99
0 20 40 60 80 100 120 140 160
Storage (MG)
Figure 2.8 Frequency distribution of required storage plotted on arithmetic-probability paper. Conversion factors:
1MG = 1,000,000 gal = 3.785 ML = 3,785,000 L.
2. The storage requirements reached or exceeded once in 20, 50, and 100 years, or 5%, 2%, and 1% of the time, are read as 123,
137,and 146 MG, respectively (466, 519, and 553 ML, respectively). Probability paper is used because it offers a rational
basis for projecting the information beyond the period of experience. The once-in-20-years requirement with 25% reserve
2
2
suggests a design storage of 123/0.75 = 164 MG/mi (230 ML/km ) of drainage area.
factor for reservoir area; D = equivalent draft, in./year or The values of A (total catchment area) and a (reservoir
e
2
2
cm/year; (MGD/mi or MLD/km ); F = adjusted flow line surface area) obtained are used as follows in recalculating
at spillway level, in. or cm; A = effective catchment area, storage requirements: Q replaces Q; D + D replaces D;
e
r
e
2
mi 2 or km ; D ed = effective draft, MGD or MLD; and and A replaces A. A fourth allowance calls for raising the
e
D md = mean draft, MGD or MLD. flow line of the reservoir by Q + E − R, expressed in units of