Page 48 - Water Engineering Hydraulics, Distribution and Treatment

26
Water Sources: Surface Water
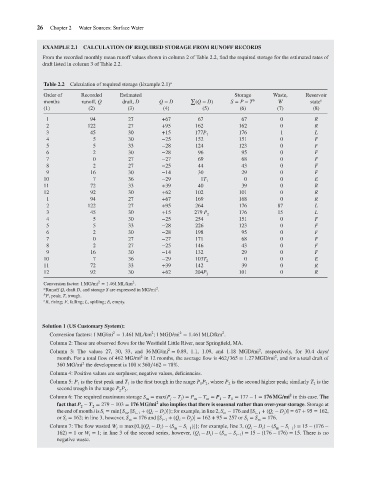
EXAMPLE 2.1 CALCULATION OF REQUIRED STORAGE FROM RUNOFF RECORDS
From the recorded monthly mean runoff values shown in column 2 of Table 2.2, find the required storage for the estimated rates of
draft listed in column 3 of Table 2.2.
Table 2.2
Recorded
Storage
Estimated
Order of
c
runoff, Q
draft, D
Q − D
W
state
months
(1)
(2)
(6)
(7)
(8)
(3)
(4)
(5)
1
27
R
94
0
67
+67
67
0
122
162
R
+95
2 Chapter 2 Calculation of required storage (Example 2.1) a ∑ (Q − D) S = P − T b Waste, Reservoir
27
162
3 45 30 +15 177P 176 1 L
1
4 5 30 −25 152 151 0 F
5 5 33 −28 124 123 0 F
6 2 30 −28 96 95 0 F
7 0 27 −27 69 68 0 F
8 2 27 −25 44 43 0 F
9 16 30 −14 30 29 0 F
10 7 36 −29 1T 1 0 0 E
11 72 33 +39 40 39 0 R
12 92 30 +62 102 101 0 R
1 94 27 +67 169 168 0 R
2 122 27 +95 264 176 87 L
3 45 30 +15 279 P 2 176 15 L
4 5 30 −25 254 151 0 F
5 5 33 −28 226 123 0 F
6 2 30 −28 198 95 0 F
7 0 27 −27 171 68 0 F
8 2 27 −25 146 43 0 F
9 16 30 −14 132 29 0 F
10 7 36 −29 103T 2 0 0 E
11 72 33 +39 142 39 0 R
12 92 30 +62 204P 101 0 R
3
2
2
Conversion factor: 1 MG/mi = 1.461 ML/km .
2
a Runoff Q, draft D, and storage S are expressed in MG/mi .
b P, peak; T, trough.
c R, rising; F, falling; L, spilling; E,empty.
Solution 1 (US Customary System):
2
2
2
2
Conversion factors: 1 MG/mi = 1.461 ML/km ; 1 MGD/mi = 1.461 MLD/km .
Column 2: These are observed flows for the Westfield Little River, near Springfield, MA.
2
2
Column 3: The values 27, 30, 33, and 36 MG/mi = 0.89, 1.1, 1.09, and 1.18 MGD/mi , respectively, for 30.4 days/
2
2
month. For a total flow of 462 MG/mi in 12 months, the average flow is 462∕365 = 1.27 MGD/mi , and for a total draft of
2
360 MG/mi the development is 100 × 360∕462 = 78%.
Column 4: Positive values are surpluses; negative values, deficiencies.
Column 5: P is the first peak and T is the first trough in the range P P ,where P is the second higher peak; similarly T is the
2
1
1 2
2
1
second trough in the range P P .
2
3
2
Column 6: The required maximum storage S =max(P − T ) = P − T = P − T = 177 − 1 = 176 MG/mi in this case. The
1
m
1
j
j
m
m
2
fact that P − T = 279 − 103 = 176 MG/mi also implies that there is seasonal rather than over-year storage. Storage at
2
2
the end of month i is S =min{S ,[S i−1 + (Q − D )]}; for example, in line 2, S − 176 and [S i−1 + (Q − D )] = 67 + 95 = 162,
m
i
i
j
i
m
j
or S = 162; in line 3, however, S = 176 and [S i−1 + (Q − D )] = 162 + 95 = 257 or S = S = 176.
m
m
j
i
i
i
Column 7: The flow wasted W =max{0, [(Q − D ) − (S − S i−1 )]}; for example, line 3, (Q − D ) − (S − S i−1 ) = 15 − (176 −
m
i
m
i
i
i
i
162) = 1or W = 1; in line 3 of the second series, however, (Q − D ) − (S − S i−1 ) = 15 − (176 − 176) = 15. There is no
i
i
m
i
negative waste.