Page 444 - Water and wastewater engineering

GRANULAR FILTRATION 11-17

where v b is the backwash velocity and the Reynolds number is defined as

d
()( ) (11-13)
v s
R

The expanded porosity is calculated for each fractional size of the media and summed for the
entire bed. An approximation technique uses the 60th percentile diameter ( d 60% in m) to calculate
the Reynolds number,
vs
()(d60 % )
R (11-14)

and then calculates the expanded porosity in one step for the entire bed depth (Cleasby, 1972). A
more sophisticated model developed by Dharmarajah and Cleasby (1986) is also available.
The determination of D e is not straightforward. From Equation 11-12 , it is obvious that
the expanded bed porosity is a function of the settling velocity. The particle settling velocity is
determined by Equation 10-8 in Chapter 10. To solve Equation 10-8, the drag coefficient ( C D )
must be calculated. The drag coefficient is a function of the Reynolds number, which, in turn, is
a function of the settling velocity. Thus, the settling velocity is needed to find the settling veloc-
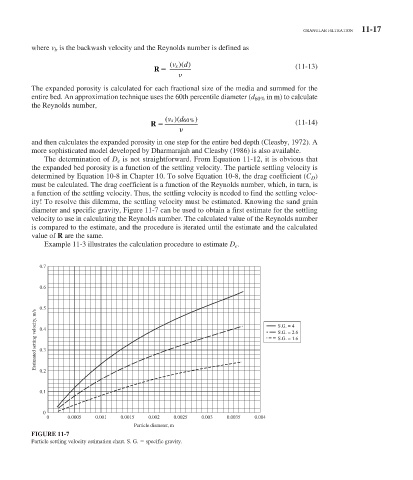
ity! To resolve this dilemma, the settling velocity must be estimated. Knowing the sand grain

diameter and specific gravity, Figure 11-7 can be used to obtain a first estimate for the settling
velocity to use in calculating the Reynolds number. The calculated value of the Reynolds number
is compared to the estimate, and the procedure is iterated until the estimate and the calculated
value of R are the same.
Example 11-3 illustrates the calculation procedure to estimate D e .

0.7

0.6

0.5
Esrimated setting velocity, m/s 0.4 S.G. = 4

S.G. = 2.6
S.G. = 1.6
0.3

0.2

0.1

0
0 0.0005 0.001 0.0015 0.002 0.0025 0.003 0.0035 0.004
Particle diameter, m
FIGURE 11-7
Particle settling velocity estimation chart. S. G. specific gravity.