Page 445 - Water and wastewater engineering

11-18 WATER AND WASTEWATER ENGINEERING

Example 11-3. Determine the depth of the expanded sand filter bed being designed for Ottawa
Island ( Example 11-2 ).

Solution. To begin, select a backwash rate. To retain the finest sand grains used in building the
filter, the backwash rate must not wash out particles with a diameter of 0.000126 m (0.0126 cm).
Using Figure 11-7 , find that for a 0.0126 cm particle with a specific gravity of 2.65, the terminal
settling velocity is approximately 1 cm/s (864 m/d).
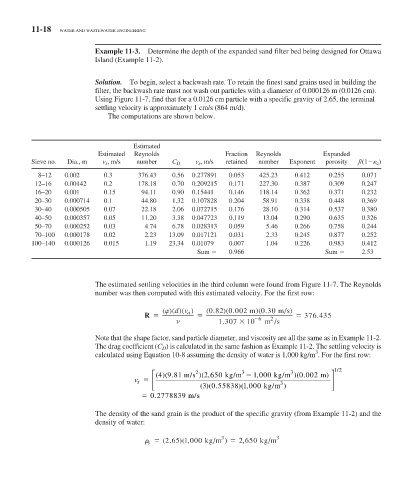
The computations are shown below.

Estimated
Estimated Reynolds Fraction Reynolds Expanded
Sieve no. Dia., m v s , m/s number C D v s , m/s retained number Exponent porosity f/(1 e )

8–12 0.002 0.3 376.43 0.56 0.277891 0.053 425.23 0.412 0.255 0.071
12–16 0.00142 0.2 178.18 0.70 0.209215 0.171 227.30 0.387 0.309 0.247
16–20 0.001 0.15 94.11 0.90 0.15441 0.146 118.14 0.362 0.371 0.232
20–30 0.000714 0.1 44.80 1.32 0.107828 0.204 58.91 0.338 0.448 0.369
30–40 0.000505 0.07 22.18 2.06 0.072715 0.176 28.10 0.314 0.537 0.380
40–50 0.000357 0.05 11.20 3.38 0.047723 0.119 13.04 0.290 0.635 0.326
50–70 0.000252 0.03 4.74 6.78 0.028313 0.059 5.46 0.266 0.758 0.244
70–100 0.000178 0.02 2.23 13.09 0.017121 0.031 2.33 0.245 0.877 0.252
100–140 0.000126 0.015 1.19 23.34 0.01079 0.007 1.04 0.226 0.983 0.412
Sum 0.966 Sum 2.53

The estimated settling velocities in the third column were found from Figure 11-7 . The Reynolds
number was then computed with this estimated velocity. For the first row:

d
()()( ) (082. )(0 002. m )(030. m/s )
v a
R
376 435
.
2
1307 10 6 m/s
7
.
Note that the shape factor, sand particle diameter, and viscosity are all the same as in Example 11-2 .
The drag coefficient ( C D ) is calculated in the same fashion as Example 11-2 . The settling velocity is
3
calculated using Equation 10-8 assuming the density of water is 1,000 kg/m . For the first row:
/
⎡ () ( . 2 2 650 kg/m 3 1 000 kg/m, 3 3 )( 0 002 m ⎤ 12
,
49 81 m/s )(
.
)
v s ⎢ 3 ⎥
⎣ () ( . ) ( , ) ⎦
3 0 55838 1 000 kg/m
0 2778839 m/s
.
The density of the sand grain is the product of the specific gravity (from Example 11-2 ) and the
density of water:
.
s (2 65 )(1 000 kg/m 3 ) 2 650 kg/m 3
,
,