Page 309 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
QC: —/—
P1: KVU/KXT
P2: KVU/KXT
20:46
AT029-Manual-v7.cls
AT029-06
June 22, 2007
AT029-Manual
6. THERMODYNAMIC RELATIONS FOR PROPERTY ESTIMATIONS 289

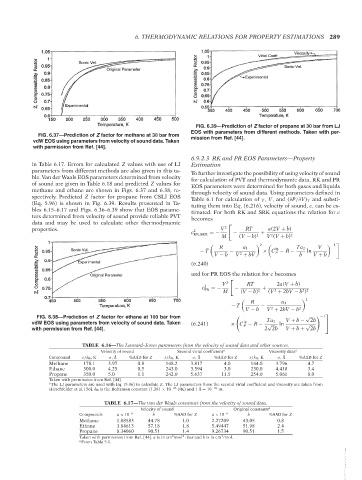
FIG. 6.39—Prediction of Z factor of propane at 30 bar from LJ
EOS with parameters from different methods. Taken with per-
FIG. 6.37—Prediction of Z factor for methane at 30 bar from
vdW EOS using parameters from velocity of sound data. Taken mission from Ref. [44].
with permission from Ref. [44].
6.9.2.3 RK and PR EOS Parameters—Property
in Table 6.17. Errors for calculated Z values with use of LJ Estimation
parameters from different methods are also given in this ta- To further investigate the possibility of using velocity of sound
ble. Van der Waals EOS parameters determined from velocity for calculation of PVT and thermodynamic data, RK and PR
of sound are given in Table 6.18 and predicted Z values for EOS parameters were determined for both gases and liquids
methane and ethane are shown in Figs. 6.37 and 6.38, re- through velocity of sound data. Using parameters defined in
spectively. Predicted Z factor for propane from CSLJ EOS Table 6.1 for calculation of γ , V, and (∂P/∂V) T and substi-
(Eq. 5.96) is shown in Fig. 6.39. Results presented in Ta- tuting them into Eq. (6.216), velocity of sound, c, can be es-
bles 6.15–6.17 and Figs. 6.36–6.39 show that EOS parame- timated. For both RK and SRK equations the relation for c
ters determined from velocity of sound provide reliable PVT becomes
data and may be used to calculate other thermodynamic
properties. 2 V 2 RT a(2V + b)
c RK,SRK =− − +
2
M (V − b) 2 V (V + b) 2
2 −1
R a 1 ig Ta 2 V

− T − × C − R − ln
P
V − b V + bV b V + b
2
(6.240)
and for PR EOS the relation for c becomes

V 2 RT 2a(V + b)
2
c PR =− − +
2 2
2
M (V − b) 2 (V + 2bV − b )
R a 1
2
− T −
V − b V + 2bV − b 2
2
FIG. 6.38—Prediction of Z factor for ethane at 100 bar from √ −1 ⎤
Ta 2
ig
vdW EOS using parameters from velocity of sound data. Taken (6.241) × C − R − √ ln V + b − √ 2b ⎦
P
with permission from Ref. [44]. 2 2b V + b + 2b
TABLE 6.16—The Lennard–Jones parameters from the velocity of sound data and other sources.
Velocity of sound Second virial coefficient a Viscosity data a
Compound ε/k B ,K σ, ˚ A %AAD for Z ε/k B ,K σ, ˚ A %AAD for Z ε/k B ,K σ, ˚ A %AAD for Z
Methane 178.1 3.97 0.8 148.2 3.817 4.0 144.0 3.796 4.7
Ethane 300.0 4.25 0.5 243.0 3.594 3.0 230.0 4.418 3.4
Propane 350.0 5.0 1.1 242.0 5.637 11.5 254.0 5.061 8.0
Taken with permission from Ref. [44].
a The LJ parameters are used with Eq. (5.96) to calculate Z. The LJ parameters from the second virial coefficient and viscosity are taken from
Hirschfelder et al. [56]. k B is the Boltzman constant (1.381 × 10 −23 J/K) and 1 ˚ A = 10 −10 m.
TABLE 6.17—The van der Waals constants from the velocity of sound data.
Velocity of sound Original constants a
Compounds a × 10 −6 b %AAD for Z a × 10 −6 b %AAD for Z
Methane 1.88583 44.78 1.0 2.27209 43.05 0.8
Ethane 3.84613 57.18 1.8 5.49447 51.98 2.4
Propane 8.34060 90.51 1.4 9.26734 90.51 1.5
6
2
3
Taken with permission from Ref. [44]. a is in cm /mol · bar and b is in cm /mol.
a From Table 5.1.
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT