Page 308 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

QC: —/—
P2: KVU/KXT
T1: IML
P1: KVU/KXT
AT029-06
20:46
288 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
where B = dB/dT and C = dC/dT. Substituting for B

C HS AT029-Manual AT029-Manual-v7.cls June 22, 2007 HS and
from Eq. (6.231) into Eq. (6.234) and, combining with
Eq. (6.229), gives two nonhomogeneous differential equa-
tions that after their solutions we get:
ln T 3 p n
B(T) = q 0 +
T T n
(6.235) n=0
ln T 3 L n
C(T) = q 1 + n
T T
n=0
Parameters p 1 and L 1 are constants of integration while
all other constants are related to parameters d 0 and d 1 in
Eq. (6.229) [44]. For example, parameters q 0 and L 0 are FIG. 6.35—Prediction of second virial coefficient of methane
from velocity of sound data (Eq. 6.239). Taken with permission
related to d 0 and d 1 as follows: q 0 = 2π N A d 0 d 1 and L 0 = from Ref. [44].
2
2 6
(5/18)π N d , where N A is the Avogadro’s number. Substitu-
A 0
tion of the truncated virial EOS, Eq. (5.76), into Eq. (6.216)
gives the following relation for the velocity of sound in terms where B is in cm /mol and T is in kelvin. This equation can
3
of virial coefficients: be fairly approximated by the following simpler form for the
γ RT second virial coefficient:
2
(6.236) c = [1 + ρ(2B + 3Cρ)]
6
6
M 10 × ln T 10 × c
(6.239) B(T) = a − b −
where γ is the heat capacity ratio (C P /C V ) and ρ is the molar T T
density (1/V). Once B and C are determined from Eq. (6.235), where B is in cm /mol and T is in kelvin. All three constants
3
C P and C V can be calculated from Eqs. (6.64) and (6.65) and a, b, and c have been directly determined from velocity of
upon substitution into Eq. (6.236) one can calculate velocity sound data for methane, ethane, and propane and are given
of sound. Vice versa the sonic velocity data can be used to in Table 6.15. When this equation is used to calculate c from
obtain virial coefficients and consequently constants p 1 and Eq. (6.236) with C = 0, an error of 0.5% was obtained for 150
L 1 in Eqs. (6.235) by minimizing the following objective data points for methane [44]. If virial equation with coeffi-
function: cients B and C (Eq. 5.76) were used obviously lower error
N
2 could be obtained. Errors for prediction of compressibility
(6.237) RC = (c i,calc. − c i,exp. ) factor of each compound using Eq. (5.75) with coefficient B
i=1
estimated from Eq. (6.239) are also given in Table 6.15. Graph-
where N is the number of data points on the velocity of sound. ical evaluation of predicted coefficient B for methane from
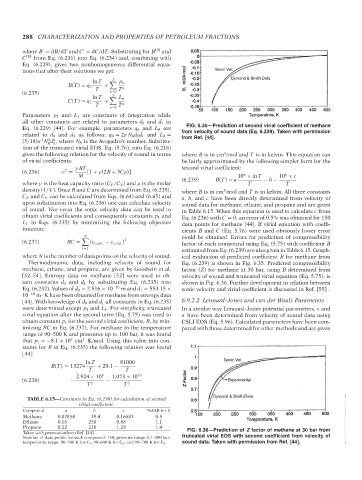
Thermodynamic data, including velocity of sound for Eq. (6.239) is shown in Fig. 6.35. Predicted compressibility
methane, ethane, and propane, are given by Goodwin et al. factor (Z) for methane at 30 bar, using B determined from
[52–54]. Entropy data on methane [52] were used to ob- velocity of sound and truncated virial equation (Eq. 5.75), is
tain constants d 0 and d 1 by substituting Eq. (6.235) into shown in Fig. 6.36. Further development in relation between
Eq. (6.232). Values of d 0 = 2.516 × 10 −10 m and d 1 = 554.15 × sonic velocity and virial coefficient is discussed in Ref. [55] .
10 −10 m · K have been obtained for methane from entropy data
[44]. With knowledge of d 0 and d 1 all constants in Eq. (6.235) 6.9.2.2 Lennard–Jones and van der Waals Parameters
were determined except p 1 and L 1 . For simplicity, truncated In a similar way Lennard–Jones potential parameters, ε and
virial equation after the second term (Eq. 5.75) was used to σ have been determined from velocity of sound data using
obtain constant p 1 for the second virial coefficient, B, by min- CSLJ EOS (Eq. 5.96). Calculated parameters have been com-
imizing RC in Eq. (6.237). For methane in the temperature pared with those determined for other methods and are given
range of 90–500 K and pressures up to 100 bar, it was found
3
3
that p 1 =−8.1 × 10 cm · K/mol. Using this value into con-
stants for B in Eq. (6.235) the following relation was found
[44]:
ln T 81000
B(T) = 13274 + 20.1 −
T T
2.924 × 10 6 1.073 × 10 10
(6.238) − −
T 2 T 3
TABLE 6.15—Constants in Eq. (6.239) for calculation of second
virial coefficient.
Compound a b c %AAD for Z
Methane 0.02854 19.4 0.16582 0.5 --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Ethane 0.16 250 0.88 1.1
Propane 0.22 230 1.29 1.4
Taken with permissionfrom Ref. [44]. FIG. 6.36—Prediction of Z factor of methane at 30 bar from
Number of data points for each compound: 150; pressure range: 0.1–200 bar; truncated virial EOS with second coefficient from velocity of
temperature range: 90–500 K for C 1 , 90–600 K for C 2 , and 90–700 K for C 3 . sound data. Taken with permission from Ref. [44].

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT