Page 306 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: KVU/KXT
QC: —/—
T1: IML
P1: KVU/KXT
20:46
June 22, 2007
AT029-06
AT029-Manual
AT029-Manual-v7.cls
286 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
equation V is the specific volume then parameter M must be
removed from the relation. Equivalent forms of this equation
in terms of specific volume or mass density are also commonly
used in various sources. From thermodynamic relations the
above relation can be converted to the following form:
γ V 2 ∂P γ ∂P
2
(6.216) c =− =
M ∂V T M ∂ρ T
where V is the molar volume, ρ is the molar density (1/V),
and γ is the heat capacity ratio (C P /C V ). Using definition of
isothermal compressibility, κ, (Eq. 6.25), the velocity of sound
can be calculated from the following relation:
γ
2
(6.217) c =
Mρκ
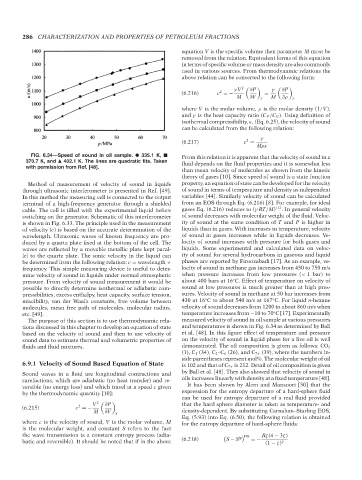
FIG. 6.34—Speed of sound in oil sample. 335.1 K, From this relation it is apparent that the velocity of sound in a
370.7 K, and 402.1 K. The lines are quadratic fits. Taken fluid depends on the fluid properties and it is somewhat less
with permission from Ref. [48].
than mean velocity of molecules as shown from the kinetic
theory of gases [10]. Since speed of sound is a state function
Method of measurement of velocity of sound in liquids property, an equation of state can be developed for the velocity
through ultrasonic interferometer is presented in Ref. [49]. of sound in terms of temperature and density as independent
In this method the measuring cell is connected to the output variables [44]. Similarly velocity of sound can be calculated
terminal of a high-frequency generator through a shielded from an EOS through Eq. (6.216) [8]. For example, for ideal
cable. The cell is filled with the experimental liquid before gases Eq. (6.216) reduces to (γ RT/M) 1/2 . In general velocity
switching on the generator. Schematic of this interferometer of sound decreases with molecular weight of the fluid. Veloc-
is shown in Fig. 6.33. The principle used in the measurement ity of sound at the same condition of T and P is higher in
of velocity (c) is based on the accurate determination of the liquids than in gases. With increases in temperature, velocity
wavelength. Ultrasonic waves of known frequency are pro- of sound in gases increases while in liquids decreases. Ve-
duced by a quartz plate fixed at the bottom of the cell. The locity of sound increases with pressure for both gases and
waves are reflected by a movable metallic plate kept paral- liquids. Some experimental and calculated data on veloc-
lel to the quartz plate. The sonic velocity in the liquid can ity of sound for several hydrocarbons in gaseous and liquid
phases are reported by Firoozabadi [17]. As an example, ve-
be determined from the following relation: c = wavelength ×
frequency. This simple measuring device is useful to deter- locity of sound in methane gas increases from 450 to 750 m/s
mine velocity of sound in liquids under normal atmospheric when pressure increases from low pressures (< 1 bar) to
◦
pressure. From velocity of sound measurement it would be about 400 bars at 16 C. Effect of temperature on velocity of
possible to directly determine isothermal or adiabatic com- sound at low pressures is much greater than at high pres-
pressibilities, excess enthalpy, heat capacity, surface tension, sures. Velocity of sound in methane at 50 bar increases from
◦
miscibility, van der Waal’s constants, free volume between 430 at 16 C to about 540 m/s at 167 C. For liquid n-hexane
◦
molecules, mean free path of molecules, molecular radius, velocity of sound decreases from 1200 to about 860 m/s when
etc. [49]. temperature increases from −10 to 70 C [17]. Experimentally
◦
The purpose of this section is to use thermodynamic rela- measured velocity of sound in oil sample at various pressures
tions discussed in this chapter to develop an equation of state and temperatures is shown in Fig. 6.34 as determined by Ball
based on the velocity of sound and then to use velocity of et al. [48]. In this figure effect of temperature and pressure
sound data to estimate thermal and volumetric properties of on the velocity of sound in liquid phase for a live oil is well
fluids and fluid mixtures. demonstrated. The oil composition is given as follows: CO 2
(1), C 1 (34), C 2 –C 6 (26), and C 7+ (39), where the numbers in-
side parentheses represent mol%. The molecular weight of oil
6.9.1 Velocity of Sound Based Equation of State is 102 and that of C 7+ is 212. Detail of oil composition is given
Sound waves in a fluid are longitudinal contractions and by Ball et al. [48]. They also showed that velocity of sound in
rarefactions, which are adiabatic (no heat transfer) and re- oils increases linearly with density at a fixed temperature [48].
versible (no energy loss) and which travel at a speed c given It has been shown by Alem and Mansoori [50] that the
by the thermodynamic quantity [10]: expression for the entropy departure of a hard-sphere fluid
can be used for entropy departure of a real fluid provided
V 2 ∂P that the hard sphere diameter is taken as temperature- and
2
(6.215) c =−
M ∂V S density-dependent. By substituting Carnahan–Starling EOS,
Eq. (5.93) into Eq. (6.50), the following relation is obtained
where c is the velocity of sound, V is the molar volume, M for the entropy departure of hard-sphere fluids:
is the molecular weight, and constant S refers to the fact
the wave transmission is a constant entropy process (adia- ig HS Rζ(4 − 3ζ)

batic and reversible). It should be noted that if in the above (6.218) S − S =− (1 − ζ) 2

--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT