Page 105 -

2.4 The Biharmonic Equation 89

Eigenspaces ◦ σ for none * satisfying none ' & p ∈ p , ∂p ∂n ◦ σ for none * satisfying ◦ 1 , σ 2 , σ 3 ◦ ◦ σ ' & p ∈ p , ∂p ∂n none

∗
=0 =0 A 1 .
ds ds =
A 0
conditions + σ 2 v ∂n ∈ v + ψ 2 v ∂n ∈ v = σ 2 ds + σ 2 x)ds given p(x)given

Side σ 1 ∂v Γ all for none ψ 1 ∂v Γ all for − Γ (σ 1 n Γ A 0 , A 1 none,

Equation ' ' p(x) ∂n p(x)

Biharmonic ' ' ψ 2 ' '& ϕ 1 + K 22 ϕ 2 V 12 ' ϕ 2 ' '& ψ 1 ψ 2 & ' + ∂ ψ 2

the '& ϕ 1 ϕ 2 ' ϕ 2 '& ψ 1 '& ψ 1 ψ 2 1 I 2 '& ϕ 1 D 32 D 42 + K 44 '& ψ 1 V 14 V 24
for − K 22 −V 12 '& ϕ 1 D 32 D 42 1 I − K 44 2 −V 34 V 14 V 24 D 21 − K 11 & D 31 D 41 1 I 2 V 34 & V 13 V 23
Equations 1 I −D 21 2 + K 11 & D 31 D 41 −D 43 + K 33 & V 13 ' u = ∂u V 23 ∂n & − = 1 I 2 ' − = σ 2 D 43 1 I − K 33 2 ' u − = ∂u ∂n

Integral & ' = 1 I σ 2 2 ' −V 34 = − K 44 & ' u = 1 I ∂u 2 ∂n '& −V 12 − K 22 & ' ∂ ∂n p ' − p σ 2 '& σ 1 V 34 + K 44 & ' u − = ∂u ∂n '& V 12 + K 22

Boundary BIEs of '& σ 1 V 24 V 14 + K 33 1 I −D 43 2 '& D 42 D 32 + K 11 1 I −D 21 2 '& σ 1 V 24 V 14 − K 33 1 I D 43 2 '& D 42 D 32 − K 11 1 I D 21 2

2.4.5. Systems & V 23 (1) V 13 & 1 I 2 (2) & D 41 (1) D 31 & 1 I 2 (2) & V 23 (1) V 13 & 1 I 2 (2) & D 41 (1) D 31 & 1 I 2 (2)

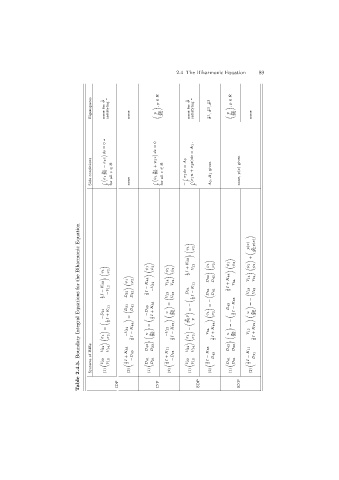
Table IDP INP EDP ENP