Page 131 - A Practical Companion to Reservoir Stimulation

PRACTICAL COMPANION TO RESERVOIR STIMULATION

EXAMPLE H-9
injection rate changes, then while the transient model is
Calculation of the Skin-Effect Evolution immune to this change, the steady-state assumption of an acid
bank of finite radius cannot handle the change. To accommo-
Using the "observed" injection pressure history shown in Fig. date the reduced rate, an increase in the calculated skin effect
H-3, plot the evolution of the skin effect using the transient will result.
and steady-state simulated injection pressures at zero skin
effect. Use the results in Example H-8.

Solution (Ref. Sections 16-3,16-4 and 16-6)
Equation 16- 15 can be used to calculate the evolution of the
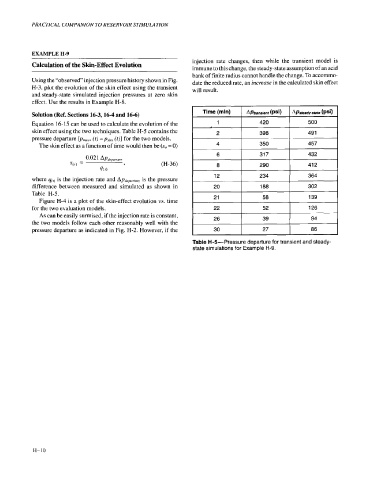
skin effect using the two techniques. Table H-5 contains the
pressure departure [p,,,.T (t) - psirll (t)] for the two models.
The skin effect as a function of time would then be (so = 0)

0.02 1 APdupl"a'<,
q r ) = (H-36)
4( I)
where q(,, is the injection rate and Ap~epar,rrr, the pressure
is
difference between measured and simulated as shown in
Table H-5.
Figure H-4 is a plot of the skin-effect evolution vs. time
for the two evaluation models.
As can be easily surmised, if the injection rate is constant,
the two models follow each other reasonably well with the
pressure departure as indicated in Fig. H-2. However, if the
Table H-5-Pressure departure for transient and steady-
state simulations for Example H-9.

H- 10