Page 267 - Adsorbents fundamentals and applications

252 CARBON NANOTUBES, PILLARED CLAYS, AND POLYMERIC RESINS

The interesting idea of separating enantiomers via chiral separation with car-
bon nanotubes was suggested and examined by Sholl and co-workers (Power
et al., 2002). A Monte Carlo technique was used to calculate the isosteric heats
of adsorption for enantiomers of trans-1,2-dimethylcyclopropane (DMCP) and
trans-1,2-dimethylcyclohexane (DMCH) inside SWNTs. Sholl and colleagues
used tubes of different diameters as well as different chiral angles. Tube diameters
◦
ranging from 9.5 ˚ A to 28.7 ˚ A and chiral angles from 34 to 54 were examined.
Unfortunately, the isosteric heats of adsorption for the two pairs of enantiomers
were negligible in all cases.

Kinetic Separations. As discussed in Chapter 5, carbon molecular sieves have
already been used for gas separation that is based on differences in diffusivities of
different gas molecules. The same separations should also be possible with carbon
nanotubes. To this end, a number of simulation studies have been carried out.
Mao and Sinnott (2000 and 2001) have reported molecular dynamics simulation
results for diffusion of methane, ethane, n-butane, and isobutene, as well as their
binary mixtures, in SWNTs and their bundles. As expected, diffusion of smaller
molecules is faster, for example a factor of 25 was obtained for methane/isobutene
in a (8,8) nanotube (Mao and Sinnott, 2001).
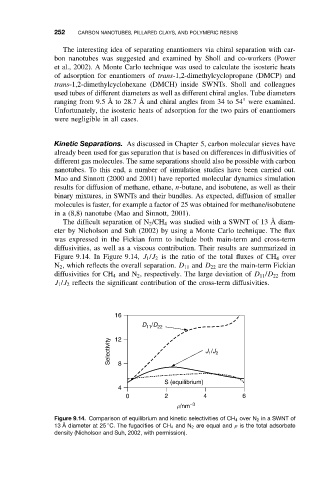
The difficult separation of N 2 /CH 4 was studied with a SWNT of 13 ˚ Adiam-
eter by Nicholson and Suh (2002) by using a Monte Carlo technique. The flux
was expressed in the Fickian form to include both main-term and cross-term
diffusivities, as well as a viscous contribution. Their results are summarized in
Figure 9.14. In Figure 9.14, J 1 /J 2 is the ratio of the total fluxes of CH 4 over
N 2 , which reflects the overall separation. D 11 and D 22 are the main-term Fickian
diffusivities for CH 4 and N 2 , respectively. The large deviation of D 11 /D 22 from
J 1 /J 2 reflects the significant contribution of the cross-term diffusivities.

16
D /D 22
11
Selectivity 12 8 J /J 2
1

S (equilibrium)
4
0 2 4 6
r/nm −3
Figure 9.14. Comparison of equilibrium and kinetic selectivities of CH 4 over N 2 in a SWNT of
◦
13 ˚ Adiameter at25 C. The fugacities of CH 4 and N 2 are equal and ρ is the total adsorbate
density (Nicholson and Suh, 2002, with permission).