Page 594 - Advanced_Engineering_Mathematics o'neil

574 CHAPTER 16 The Wave Equation

0.4

0
0 0.5 1 1.5 2 2.5 3
x

–0.4

–0.8

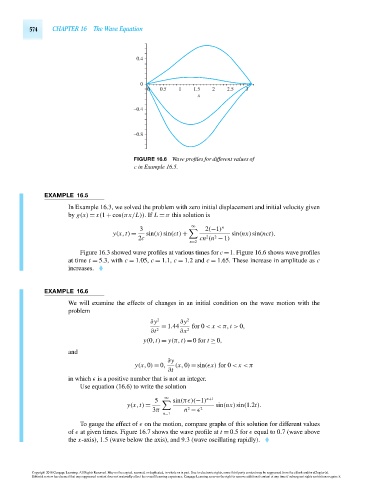
FIGURE 16.6 Wave profiles for different values of
c in Example 16.5.

EXAMPLE 16.5
In Example 16.3, we solved the problem with zero initial displacement and initial velocity given
by g(x) = x(1 + cos(πx/L)).If L = π this solution is
∞ n
3
2(−1)
y(x,t) = sin(x)sin(ct) + sin(nx)sin(nct).
2
2c cn (n − 1)
2
n=2
Figure 16.3 showed wave profiles at various times for c =1. Figure 16.6 shows wave profiles
at time t = 5.3, with c = 1.05, c = 1.1, c = 1.2 and c = 1.65. These increase in amplitude as c
increases.

EXAMPLE 16.6

We will examine the effects of changes in an initial condition on the wave motion with the
problem
∂y 2 ∂y 2
= 1.44 for 0 < x <π,t > 0,
∂t 2 ∂x 2
y(0,t) = y(π,t) = 0for t ≥ 0,
and
∂y
y(x,0) = 0, (x,0) = sin( x) for 0 < x <π
∂t
in which is a positive number that is not an integer.
Use equation (16.6) to write the solution

∞
5
sin(π )(−1) n+1
y(x,t) = sin(nx)sin(1.2t).
3π n − 2
2
n=1
To gauge the effect of on the motion, compare graphs of this solution for different values
of at given times. Figure 16.7 shows the wave profile at t = 0.5for equal to 0.7 (wave above
the x-axis), 1.5 (wave below the axis), and 9.3 (wave oscillating rapidly).

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:23 THM/NEIL Page-574 27410_16_ch16_p563-610