Page 66 - Advanced Gas Turbine Cycles

42 Advanced gas turbine cycles

1.4
z
(I)
I
0
ti
1.3
v)
U
0
P
3g
p E1.2 - FUEL-AIR RATIO 0.0
“3
Y,
c
-J Y -- -FUELAIR RATIO 0.0135
n
0
1.1
I - FUEL-AIR RATIO 0.027
0
LL
E
n
v)
1
200 400 600 800 1000 1200 1400 1600 1800
TEMPERATURE K
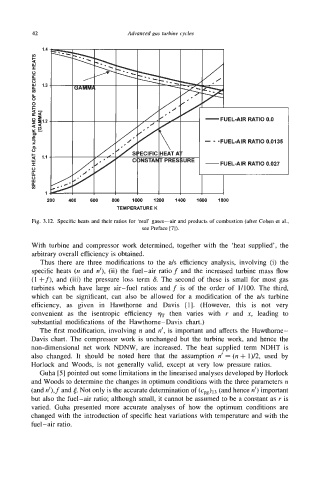
Fig. 3.12. Specific heats and their ratios for ‘real’ gases-air and products of combustion (after Cohen et al.,
see Preface 171).
With turbine and compressor work determined, together with the ‘heat supplied’, the
arbitrary overall efficiency is obtained.
Thus there are three modifications to the ah efficiency analysis, involving (i) the
specific heats (n and n’), (ii) the fuel-air ratio f and the increased turbine mass flow
(1 +fl, and (iii) the pressure loss term 8. The second of these is small for most gas
turbines which have large air-fuel ratios and f is of the order of 1/100. The third,
which can be significant, can also be allowed for a modification of the a/s turbine
efficiency, as given in Hawthorne and Davis [I]. (However, this is not very
convenient as the isentropic efficiency then varies with r and x, leading to
substantial modifications of the Hawthome-Davis chart.)
The first modification, involving n and n’, is important and affects the Hawthome-
Davis chart. The compressor work is unchanged but the turbine work, and hence the
non-dimensional net work NDNW, are increased. The heat supplied term NDHT is
also changed. It should be noted here that the assumption n’ = (n + l)/2, used by
Horlock and Woods, is not generally valid, except at very low pressure ratios.
Guha [5] pointed out some limitations in the linearised analyses developed by Horlock
and Woods to determine the changes in optimum conditions with the three parameters n
(and
(and n’),f and 6. Not only is the accurate determination of (c~~),~ hence n’) important
but also the fuel-air ratio; although small, it cannot be assumed to be a constant as r is
varied. Guha presented more accurate analyses of how the optimum conditions are
changed with the introduction of specific heat variations with temperature and with the
fuel-air ratio.