Page 182 - Advanced Thermodynamics for Engineers, Second Edition

8.3 LAW OF CORRESPONDING STATES 169

Substituting the values of p c and T c into these terms gives
3 2 2
27 8:3143 10 18 ð374:1 þ 273Þ 6 2 6 2
a ¼ 5 ¼ 1703:4Pa m =kg ¼ 0:017034 bar m =kg
64 221:2 10
3
8:3143 10 ð374:1 þ 273Þ 3
b ¼ 5 ¼ 0:0016891 m =kg
18 8 221:2 10
which results in the following van der Waals equation for water
0:004619T 0:017034
p ¼ (8.27)
ðv 0:0016891Þ v 2
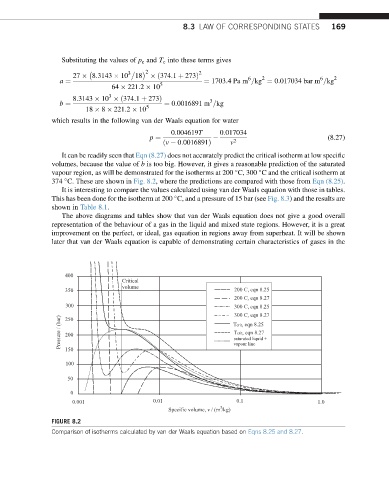
It can be readily seen that Eqn (8.27) does not accurately predict the critical isotherm at low specific
volumes, because the value of b is too big. However, it gives a reasonable prediction of the saturated
vapour region, as will be demonstrated for the isotherms at 200 C, 300 C and the critical isotherm at

374 C. These are shown in Fig. 8.2, where the predictions are compared with those from Eqn (8.25).

It is interesting to compare the values calculated using van der Waals equation with those in tables.

This has been done for the isotherm at 200 C, and a pressure of 15 bar (see Fig. 8.3) and the results are
shown in Table 8.1.
The above diagrams and tables show that van der Waals equation does not give a good overall
representation of the behaviour of a gas in the liquid and mixed state regions. However, it is a great
improvement on the perfect, or ideal, gas equation in regions away from superheat. It will be shown
later that van der Waals equation is capable of demonstrating certain characteristics of gases in the

400
Critical
volume
350 200 C, eqn 8.25
200 C, eqn 8.27
300 300 C, eqn 8.25
300 C, eqn 8.27
Pressure / (bar) 200 Tcrit, eqn 8.25
250
Tcrit, eqn 8.27
saturated liquid +
vapour line
150
100

50

0
0.001 0.01 0.1 1.0
3
Specific volume, v / (m /kg)
FIGURE 8.2
Comparison of isotherms calculated by van der Waals equation based on Eqns 8.25 and 8.27.